Sorting Algorithm
Implementation and benchmarking of classic and modern sorting algorithms with a focus on performance, memory, and stability across diverse input patterns.
📄 PDF: Project PDF
Problem Statement
In many applications, sorting is a fundamental operation. While classical algorithms such as Merge Sort and Quick Sort are widely known, newer or specialized algorithms offer different trade-offs in performance, stability, and space usage.
The objective of this project is to implement and evaluate 12 sorting algorithms under unified conditions. Through benchmarking across diverse input types and data sizes, we aim to analyze their actual runtime characteristics, stability, and behavior with different data types.
However, in real-world scenarios, performance is not the only concern. For example:
- Stability is important when secondary ordering must be preserved after a primary sort.
- Many inputs may already be partially or fully sorted, and some algorithms can take advantage of such structure.
- Applications often involve sorting not only integers, but also long integers, floating point numbers, or doubles.
- In environments with limited memory, algorithms with in-place behavior or lower space complexity may be preferable.
This project investigates not just the theoretical complexity, but practical trade-offs across different algorithmic dimensions. It is designed to provide insights into:
- Which algorithms perform best under which conditions
- How data characteristics influence performance and correctness
All implementations are CPU-based, focusing on algorithmic behavior without relying on hardware-level optimizations.
Basic Sorting Algorithms
This section reviews six classical sorting algorithms:
- Merge Sort
- Heap Sort
- Bubble Sort
- Insertion Sort
- Selection Sort
- Quick Sort
Merge Sort
Merge Sort is a classical divide-and-conquer algorithm introduced by John von Neumann in 1945. It recursively splits the input array into two halves, sorts them independently, and then merges the sorted halves. This top-down recursive structure ensures consistent performance across all input distributions, making it suitable for general-purpose use.
Pseudocode
\begin{algorithm}
\caption{MergeSort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A, indices left, right
\IF{left < right}
\STATE mid := floor((left + right) / 2)
\STATE \CALL{MergeSort}{A, left, mid}
\STATE \CALL{MergeSort}{A, mid + 1, right}
\STATE \CALL{Merge}{A, left, mid, right}
\ENDIF
\end{algorithmic}
\end{algorithm}
Characteristics
- Especially effective for linked lists and external sorting (e.g., large disk-based files), because it doesn’t rely on random access.
-
Time Complexity:
- Best: O(n log n)
- Average: O(n log n)
- Worst: O(n log n)
- Space Complexity: O(n) — due to the auxiliary array used during merging
- Stability: ✅ Stable (preserves order of equal elements)
- In-place: ❌ No (requires extra memory)
Heap Sort
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements. It first builds a max-heap from the input array, and then repeatedly extracts the maximum element and moves it to the end of the array. This process continues until the entire array is sorted in-place. The algorithm was introduced by J. W. J. Williams in 1964 and further optimized by R. W. Floyd.
Pseudocode
\begin{algorithm}
\caption{Heap Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\CALL{BuildMaxHeap}{A, n}
\FOR{i := n - 1 \DOWNTO 1}
\STATE swap A[0] and A[i]
\STATE heapSize := heapSize - 1
\CALL{MaxHeapify}{A, 0, heapSize}
\ENDFOR
\end{algorithmic}
\end{algorithm}
Characteristics
-
Unlike Merge Sort, Heap Sort does not require additional memory and operates entirely in-place.
-
It is not stable, as it swaps elements without regard to their original positions.
-
Its non-sequential memory access pattern often leads to suboptimal cache performance.
-
Nonetheless, it provides a reliable worst-case time complexity of O(n log n), making it suitable for applications requiring guaranteed upper bounds.
-
Time Complexity: Best: O(n log n), Average: O(n log n), Worst: O(n log n)
-
Space Complexity: O(1)
-
Stability: ✗ Not stable
-
In-place: ✓ Yes
Bubble Sort
Bubble Sort is a simple comparison-based algorithm that repeatedly steps through the array, compares adjacent elements, and swaps them if they are in the wrong order. This process continues until the array is fully sorted. The algorithm gets its name because smaller elements gradually “bubble up” to the front of the array through successive swaps.
Pseudocode
\begin{algorithm}
\caption{Bubble Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\FOR{i := 0 \TO n - 2}
\FOR{j := 0 \TO n - i - 2}
\IF{A[j] > A[j + 1]}
\STATE swap A[j] and A[j + 1]
\ENDIF
\ENDFOR
\ENDFOR
\end{algorithmic}
\end{algorithm}
Characteristics
-
Easy to implement and understand, but highly inefficient for large datasets due to its quadratic time complexity.
-
Mostly used for educational purposes.
-
Can achieve O(n) time when input is already sorted, but this requires an early termination check (not included in the pseudocode).
-
Time Complexity: Best: O(n) (with early termination), Average: O(n²), Worst: O(n²)
-
Space Complexity: O(1)
-
Stability: ✓ Stable
-
In-place: ✓ Yes
Insertion Sort
Insertion Sort builds the sorted array one element at a time by repeatedly picking the next element from the input and inserting it into its correct position among the previously sorted elements. It is intuitive and performs efficiently on small or nearly sorted datasets, making it a good choice for simple use cases or as a subroutine in hybrid algorithms.
Pseudocode
\begin{algorithm}
\caption{Insertion Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\FOR{i := 1 \TO n - 1}
\STATE key := A[i]
\STATE j := i - 1
\WHILE{j >= 0 and A[j] > key}
\STATE A[j + 1] := A[j]
\STATE j := j - 1
\ENDWHILE
\STATE A[j + 1] := key
\ENDFOR
\end{algorithmic}
\end{algorithm}
Characteristics
-
Particularly effective when the input is already partially sorted, requiring fewer comparisons and shifts.
-
In the best case (already sorted), each element is simply compared once, resulting in O(n) time.
-
It is also stable and in-place, making it well-suited for memory-constrained environments.
-
Time Complexity: Best: O(n), Average: O(n²), Worst: O(n²)
-
Space Complexity: O(1)
-
Stability: ✓ Stable
-
In-place: ✓ Yes
Selection Sort
Selection Sort repeatedly selects the minimum (or maximum) element from the unsorted portion and moves it to the beginning (or end) of the sorted portion. Unlike Insertion Sort, it performs fewer swaps, but makes significantly more comparisons. Its structure is simple and intuitive, which makes it useful for teaching sorting principles, though not for performance-critical applications.
Pseudocode
\begin{algorithm}
\caption{Selection Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\FOR{i := 0 \TO n - 2}
\STATE min := i
\FOR{j := i + 1 \TO n - 1}
\IF{A[j] < A[min]}
\STATE min := j
\ENDIF
\ENDFOR
\IF{min != i}
\STATE swap A[i] and A[min]
\ENDIF
\ENDFOR
\end{algorithmic}
\end{algorithm}
Characteristics
-
Inefficient for large datasets due to quadratic time complexity O(n²) regardless of input order
-
Not stable – swapping can disrupt the order of equal elements
-
In-place and performs a minimal number of writes, useful when memory writes are costly
-
Time Complexity: Best: O(n²), Average: O(n²), Worst: O(n²)
-
Space Complexity: O(1)
-
Stability: ✗ Not stable
-
In-place: ✓ Yes
Quick Sort
Quick Sort is a divide-and-conquer algorithm that recursively partitions the array around a pivot. Elements less than the pivot are moved to its left, and elements greater than the pivot to its right. In the CLRS version, the last element is used as the pivot, which can lead to highly unbalanced partitions on already sorted data.
Pseudocode
\begin{algorithm}
\caption{Quick Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A, indices low, high
\IF{low < high}
\STATE pivot := A[high]
\STATE i := low - 1
\FOR{j := low \TO high - 1}
\IF{A[j] <= pivot}
\STATE i := i + 1
\STATE swap A[i] and A[j]
\ENDIF
\ENDFOR
\STATE swap A[i + 1] and A[high]
\STATE p := i + 1
\CALL{QuickSort}{A, low, p - 1}
\CALL{QuickSort}{A, p + 1, high}
\ENDIF
\end{algorithmic}
\end{algorithm}
Characteristics
-
Simple and fast on average with expected time complexity O(n log n) when balanced partitions are formed
-
Poor pivot choice (e.g., always selecting last element on sorted input) leads to worst-case O(n²)
-
Randomized pivot selection often used to avoid unbalanced partitions
-
Time Complexity: Best: O(n log n), Average: O(n log n), Worst: O(n²)
-
Space Complexity: O(log n) (due to recursion)
-
Stability: ✗ Not stable
-
In-place: ✓ Yes
-
First Described By: C. A. R. Hoare in 1961
Advanced Sorting Algorithms
In this section, we review six advanced or modern sorting algorithms: Library Sort, Tim Sort, Cocktail Shaker Sort, Comb Sort, Tournament Sort, and Introsort.
Library Sort
Library Sort, also known as Gapped Insertion Sort, improves upon classical Insertion Sort by maintaining evenly spaced gaps within an auxiliary array. This reduces the number of element shifts during insertion and improves average-case performance.
We follow the practical scheme proposed by Faujdar and Ghrera, using an auxiliary array of size (1 + ε)n initially filled with sentinel gaps. The first element is placed at the center, and subsequent elements are inserted using gap-aware binary search on occupied positions. If the target is occupied, elements shift right until a gap is found. After every 2^i insertions, a rebalancing step evenly redistributes elements.
Pseudocode
\begin{algorithm}
\caption{Library Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\STATE initialize G as empty array of size (1 + epsilon) * n filled with GAPs
\STATE insert A[0] into center of G
\STATE inserted := 1, round := 0
\FOR{i := 1 \TO n - 1}
\IF{inserted = 2^round}
\STATE rebalance G
\STATE round := round + 1
\ENDIF
\STATE use gap-aware binary search to find insert index i
\WHILE{G[i] is occupied}
\STATE i := i + 1
\ENDWHILE
\STATE shift elements to make space at i
\STATE insert A[i] at position i
\STATE inserted := inserted + 1
\ENDFOR
\RETURN G with gaps removed
\end{algorithmic}
\end{algorithm}
Library Sort has average-case time complexity O(n log n), but may degrade to O(n²) due to excessive shifts. In ideal conditions, it can reach O(n) in the best case. It is not stable, as rebalancing disrupts the order of equal keys, and it is not in-place, requiring O((1 + ε)n) memory.
In practice, sorted inputs often trigger worst-case behavior by inducing dense insertions and frequent rebalancing. While asymptotically appealing, these limitations confine its use to experimental or pedagogical contexts.
Tim Sort
Tim Sort is a hybrid sorting algorithm that combines the strengths of Insertion Sort and Merge Sort. Originally designed by Tim Peters for Python in 2002, it is now the default in Python, Java, and Android due to its practical performance.
The algorithm partitions the input array into segments called runs, which are either naturally ordered or explicitly sorted using Insertion Sort. These sorted runs are then merged in a bottom-up manner, similar to Merge Sort.
Pseudocode
\begin{algorithm}
\caption{Tim Sort}
\begin{algorithmic}
\STATE \textbf{Input:} Array A of size n
\STATE partition A into runs of size RUN
\FOR{each run}
\STATE sort the run using Insertion Sort
\ENDFOR
\STATE runSize := RUN
\WHILE{runSize < n}
\FOR{each pair of adjacent runs}
\STATE merge them using Merge Sort logic
\ENDFOR
\STATE runSize := runSize * 2
\ENDWHILE
\RETURN fully merged and sorted array
\end{algorithmic}
\end{algorithm}
Tim Sort leverages the simplicity of Insertion Sort on small or nearly sorted subarrays and the efficiency of Merge Sort for large-scale merging. It guarantees a worst-case time complexity of O(n log n) and performs optimally on real-world data, often achieving best-case O(n) when the input is already sorted. The algorithm is also stable, preserving the relative order of equal elements.
However, Tim Sort is not in-place, requiring O(n) auxiliary space for merging. Its adaptive nature and reliable performance explain its adoption in modern standard libraries.
Cocktail Shaker Sort
Cocktail Shaker Sort, also known as Bidirectional Bubble Sort or Ripple Sort, is a variation of Bubble Sort that improves its performance slightly by sorting in both directions within each pass. It was first introduced by Edward H. Friend in 1956.
In standard Bubble Sort, larger elements “bubble” toward the end of the array via repeated adjacent swaps. Cocktail Shaker Sort enhances this behavior by also moving smaller elements toward the beginning of the list during the same iteration. Each full iteration consists of a forward pass (left to right) followed by a backward pass (right to left), which helps reduce the number of necessary iterations when the array is partially sorted.
Pseudocode
\begin{algorithm}
\caption{Cocktail Shaker Sort}
\begin{algorithmic}
\STATE Input: Array A of size n
\STATE left := 0
\STATE right := n - 1
\STATE swapped := true
\WHILE{swapped = true}
\STATE swapped := false
\FOR{i := left \TO right - 1}
\IF{A[i] > A[i + 1]}
\STATE swap A[i] and A[i + 1]
\STATE swapped := true
\ENDIF
\ENDFOR
\STATE right := right - 1
\FOR{i := right \DOWNTO left + 1}
\IF{A[i] < A[i - 1]}
\STATE swap A[i] and A[i - 1]
\STATE swapped := true
\ENDIF
\ENDFOR
\STATE left := left + 1
\ENDWHILE
\RETURN A
\end{algorithmic}
\end{algorithm}
Characteristics
- Retains the simplicity and stability of Bubble Sort
- Reduces redundant passes by sorting in both directions
- Still inefficient on large unsorted data due to quadratic time complexity O(n²)
- Performs better on partially sorted inputs
- Best-case time: O(n) (early termination)
- Stability: ✓ Stable
- In-place: ✓ Yes
- Space Complexity: O(1)
Comb Sort
Comb Sort is a refinement of Bubble Sort introduced by Włodzimierz Dobosiewicz in 1980. It addresses a key inefficiency of Bubble Sort—turtles, which are small elements near the end of the list that require many iterations to move forward.
The core idea is to compare and swap elements that are a fixed distance apart, called the gap, which decreases over time. Initially, the gap is set to the length of the array and is reduced by a shrink factor—typically around 1.3—after each pass. As the gap approaches 1, Comb Sort behaves similarly to Bubble Sort but with most large out-of-place elements already moved closer to their correct positions.
Pseudocode
\begin{algorithm}
\caption{Comb Sort}
\begin{algorithmic}
\STATE Input: Array A of size n
\STATE gap := n
\STATE shrink := 1.3
\STATE sorted := false
\WHILE{sorted = false}
\STATE gap := floor(gap / shrink)
\IF{gap <= 1}
\STATE gap := 1
\STATE sorted := true
\ENDIF
\FOR{i := 0 \TO n - gap - 1}
\IF{A[i] > A[i + gap]}
\STATE swap A[i] and A[i + gap]
\STATE sorted := false
\ENDIF
\ENDFOR
\ENDWHILE
\RETURN A
\end{algorithmic}
\end{algorithm}
Characteristics
- More efficient than Bubble Sort, especially with many small trailing elements
- Worst-case time: O(n²)
- Average-case time: O(n log n) (with good shrink factor)
- Best-case time: O(n)
- Stability: ✗ Not stable
- In-place: ✓ Yes
- Space Complexity: O(1)
Tournament Sort
Tournament Sort is a comparison-based sorting algorithm that organizes input elements into a complete binary tree structure, known as a tournament tree. Each element is initially placed at a leaf, and each internal node stores the smaller (i.e., “winning”) of its two children. The minimum element is thus located at the root.
After extracting the root, the winner’s original leaf is replaced with a sentinel value (∞), and the path from that leaf to the root is updated to reflect the new tournament result. This process is repeated n times until all elements are extracted in sorted order.
Pseudocode
\begin{algorithm}
\caption{Tim Sort}
\begin{algorithmic}
\STATE Input: Array A of size n
\STATE partition A into runs of size RUN
\FOR{each run}
\STATE sort the run using Insertion Sort
\ENDFOR
\STATE runSize := RUN
\WHILE{runSize < n}
\FOR{each pair of adjacent runs}
\STATE merge them using Merge Sort
\ENDFOR
\STATE runSize := runSize * 2
\ENDWHILE
\RETURN fully sorted array
\end{algorithmic}
\end{algorithm}
Characteristics
- Time Complexity: O(n log n) in all cases
- Space Complexity: O(n), since the tree has ≈ 2n nodes
- Stability: Can be stable if ties are broken consistently (e.g., left child preferred)
- In-place: ✗ No
- Due to its high overhead, it is rarely used for internal sorting but useful for external sorting and stream merging
Introsort
Introspective Sort, or Introsort, is a hybrid sorting algorithm introduced by David Musser. It starts with Quick Sort and switches to Heap Sort if the recursion depth exceeds a threshold (typically 2 log n), ensuring worst-case time complexity O(n log n) while preserving Quick Sort’s average-case speed.
It recursively applies Quick Sort while monitoring the call stack depth. If the depth exceeds a safe bound, it falls back to Heap Sort. For small arrays, Insertion Sort is used for efficiency.
Pseudocode
\begin{algorithm}
\caption{Tournament Sort}
\begin{algorithmic}
\STATE Input: Array A of size n
\STATE build complete binary tree T with n leaves holding elements of A
\FOR{each internal node}
\STATE store the minimum of its two children
\ENDFOR
\FOR{i := 1 \TO n}
\STATE winner := T[1] // root of the tree
\STATE output winner to result
\STATE replace winner’s original leaf with INF
\STATE update tree values upward along winner's path
\ENDFOR
\RETURN sorted result
\end{algorithmic}
\end{algorithm}
Characteristics
- Combines the strengths of Quick Sort, Heap Sort, and Insertion Sort
- Time Complexity: O(n log n) in worst case
- Space Complexity: O(log n) (recursion stack)
- Stability: ✗ Not stable
- In-place: ✓ Yes
- Used as the backend of
std::sortin C++ standard library for its robust performance on diverse inputs
Experimental Results and Analysis
Experimental Environment
All benchmarks were conducted on a MacBook Pro (2023, 14-inch) equipped with an Apple M2 Pro chip featuring a 10-core CPU, running macOS 15.4. All sorting algorithms were implemented in C++17 and compiled using Apple Clang (g++) with the -O2 optimization flag to ensure reasonable performance tuning.
The benchmarking framework was written in Python, and automated the full evaluation pipeline including compilation, execution, timing measurements, and output validation.
Performance Across Algorithms
Method. Each sorting algorithm was evaluated on the same randomly generated dataset of size n = 10⁶. The benchmark was repeated 10 times per algorithm, and the average runtime was recorded. The results show clear performance tiers and highlight the relative efficiency of each algorithm.
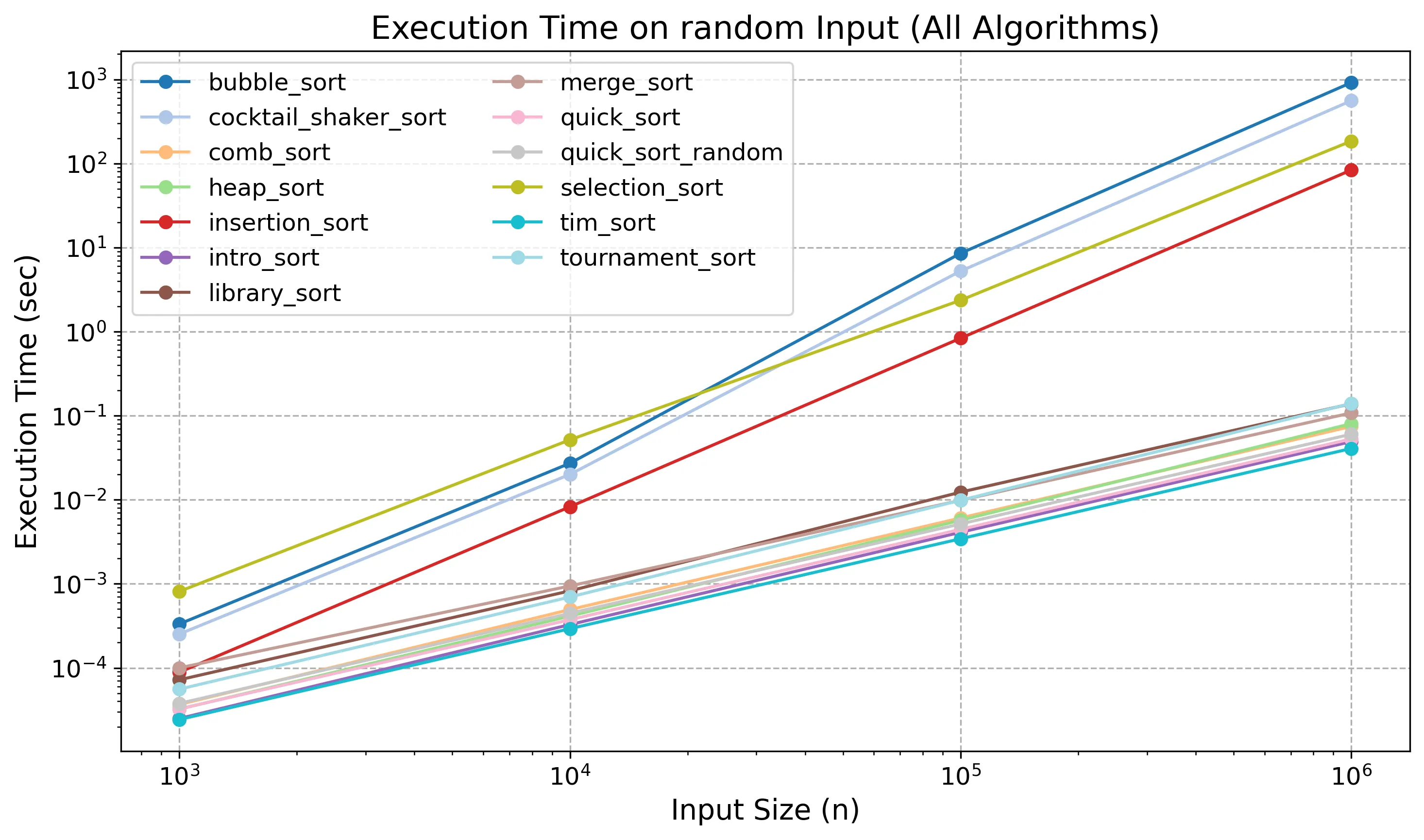
Algorithms with Log-Linear Complexity (O(n log n))
These algorithms perform efficiently even on large inputs:
-
Merge Sort Divides the array recursively and merges sorted subarrays in linear time. Consistent and stable performance makes it a reliable benchmark.
-
Heap Sort Builds a max-heap and repeatedly extracts the maximum. Avoids extra memory allocation but suffers from non-local access patterns.
-
Quick Sort (Fixed Pivot) Partitions the array using a fixed pivot (last element). Performs well on random data but degrades on sorted input due to unbalanced splits.
-
Quick Sort (Random Pivot) Uses random pivot selection to avoid worst-case splits, maintaining stable log-linear performance.
-
Intro Sort Starts as Quick Sort and switches to Heap Sort if recursion exceeds a threshold. Provides log-linear guarantees with good average performance.
-
Tim Sort Detects runs and merges them efficiently. Combines Insertion Sort (for small runs) with Merge Sort, offering real-world performance and stability.
-
Library Sort Inserts elements into a sparse array using binary search and periodic rebalancing. Approaches log-linear time but suffers from gap management overhead.
-
Comb Sort Eliminates small disorder early using shrinking gaps. Though not log-linear in worst case, performs comparably to faster algorithms on random data.
Algorithms with Quadratic Complexity (O(n²))
These become inefficient as input size grows:
-
Bubble Sort Repeatedly swaps adjacent elements, resulting in n² comparisons. Extremely inefficient.
-
Insertion Sort Builds a sorted section incrementally. Efficient on nearly sorted data but expensive on random input.
-
Selection Sort Selects the minimum in each pass. Performs many comparisons, and is consistently one of the slowest.
-
Cocktail Shaker Sort Improves Bubble Sort with bidirectional passes. Slightly reduces iterations, but still quadratic and far behind log-linear algorithms.
-
Tournament Sort Although theoretically log-linear, performs poorly in practice due to overhead from maintaining and updating a full binary tree. Each extraction involves copying full-width data, making it behave closer to quadratic under random input.
Latency for Random Inputs (in seconds)
| Algorithm | n = 10³ | n = 10⁴ | n = 10⁵ | n = 10⁶ |
|---|---|---|---|---|
| Merge Sort | 0.0001000 | 0.0009431 | 0.0098381 | 0.1078913 |
| Heap Sort | 0.0000323 | 0.0004130 | 0.0057043 | 0.0803684 |
| Bubble Sort | 0.0003324 | 0.0271842 | 8.5452850 | 916.6450000 |
| Insertion Sort | 0.0000888 | 0.0082530 | 0.8353202 | 83.6130300 |
| Selection Sort | 0.0008122 | 0.0516557 | 2.3630430 | 184.6850000 |
| Quick Sort | 0.0000325 | 0.0003742 | 0.0044425 | 0.0528438 |
| Quick Sort (Random) | 0.0000378 | 0.0004457 | 0.0051551 | 0.0602114 |
| Library Sort | 0.0000721 | 0.0008245 | 0.0123183 | 0.1386819 |
| Cocktail Shaker Sort | 0.0002524 | 0.0200263 | 5.2499610 | 558.3070000 |
| Tim Sort | 0.0000243 | 0.0002927 | 0.0034355 | 0.0407254 |
| Comb Sort | 0.0000367 | 0.0004937 | 0.0060670 | 0.0745422 |
| Tournament Sort | 0.0000558 | 0.0006971 | 0.0098557 | 0.1399134 |
| Intro Sort | 0.0000250 | 0.0003273 | 0.0040994 | 0.0491607 |
Summary. As shown in the table, the algorithms clearly separate into two performance tiers:
- Tim Sort consistently outperformed all other algorithms across all input sizes, validating its design for real-world use cases.
- Intro Sort was second fastest and notable for being the basis of
std::sortin the C++ standard library.
Performance Sensitivity to Input Order
Method. Each algorithm was tested on three types of input:
- 50% partially sorted
- Fully sorted in ascending order
- Fully sorted in descending order
All arrays were of type int, and input sizes tested were: n ∈ {10³, 10⁴, 10⁵, 10⁶}. Each test configuration was repeated 10 times, and the average runtime was reported.
These tests show how the initial structure of the data affects algorithm performance—some benefit from pre-sorted input, while others degrade.
Execution Time for 50% Partially Sorted Inputs
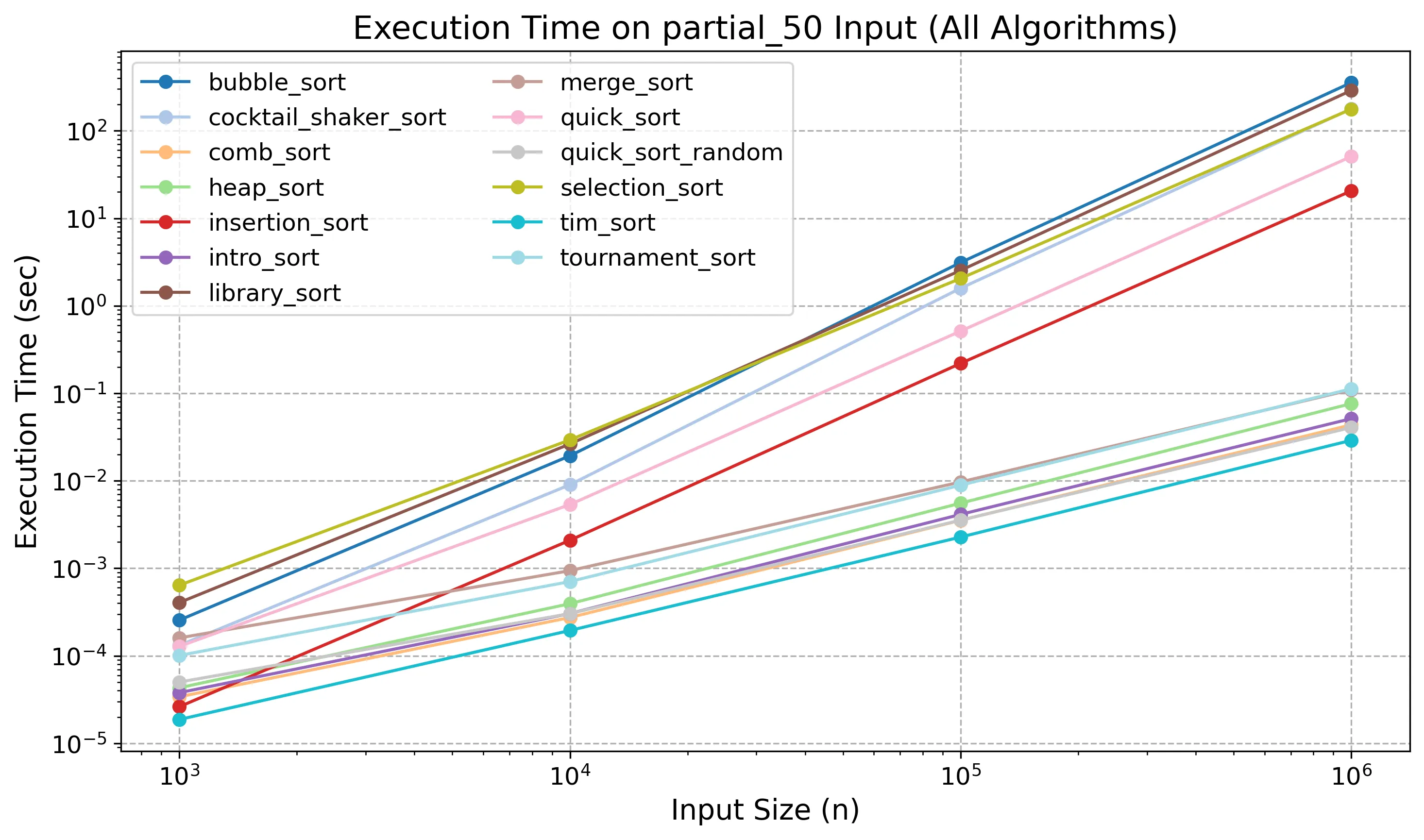
Unexpected Behavior at Small Scales On partially sorted inputs of size n = 10³, Insertion Sort ranked as the second fastest algorithm, outperforming several O(n log n) methods.
This behavior can be attributed to:
- Very low algorithmic overhead
- Tight inner loop with minimal branching
- Excellent memory locality and CPU branch prediction
For small inputs, the number of required shifts is small, while more complex algorithms like Merge Sort and Heap Sort suffer from fixed overheads such as recursion and heapification. As a result, Insertion Sort can outperform theoretically faster algorithms on small, partially ordered inputs.
Execution Time for Ascending Sorted Inputs
Ascending Sorted Inputs
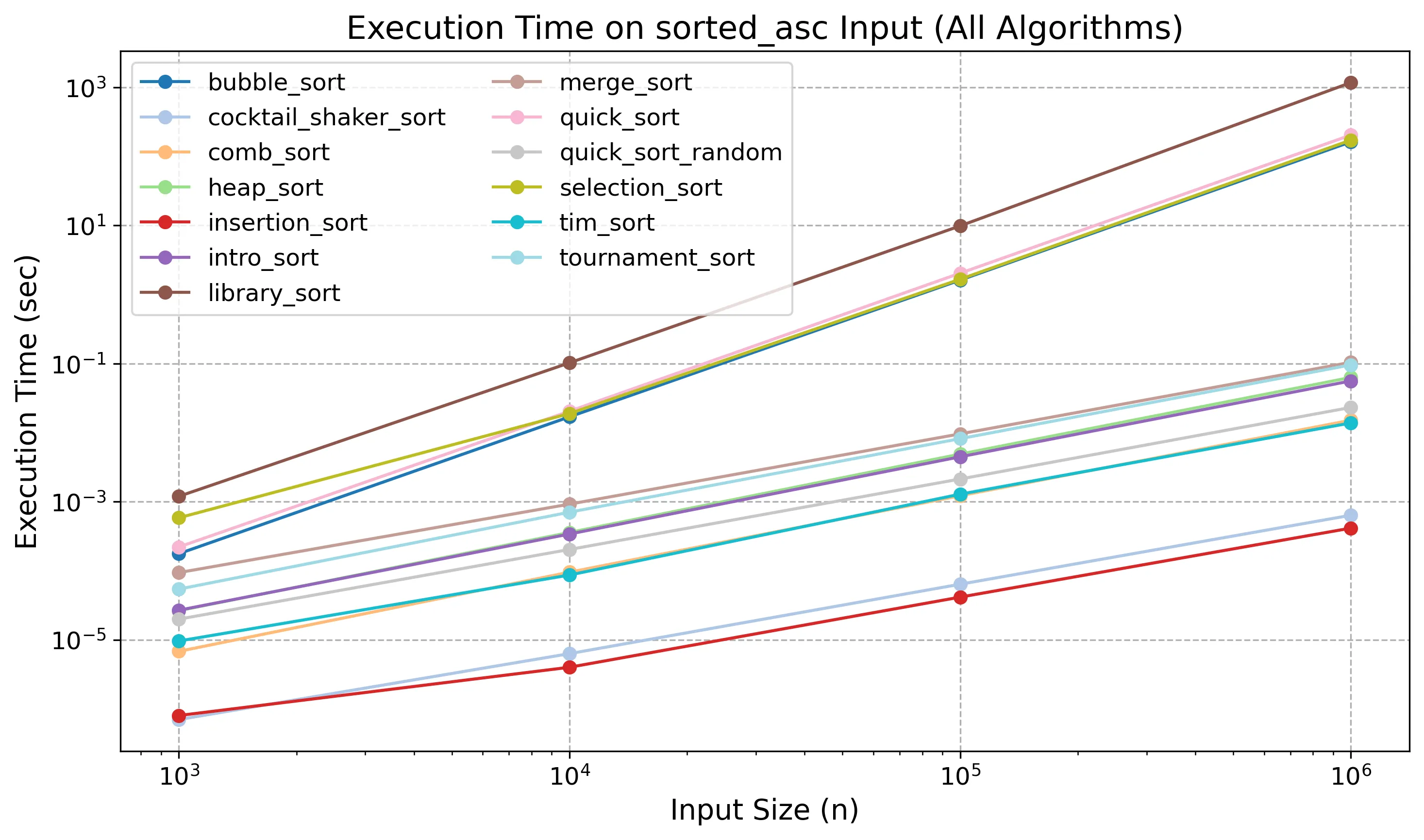
When the input is already sorted in ascending order, several algorithms achieve best-case behavior:
- Insertion Sort reaches its optimal O(n) time, with no shifts needed. Its latency becomes negligible even for large inputs.
- Cocktail Shaker Sort terminates after a single pass in each direction, also approaching linear performance.
- Quick Sort (with last-element pivot) performs poorly: sorted input causes unbalanced partitions, resulting in worst-case O(n²) behavior and large latency spikes.
- Library Sort also underperforms: although its best case is theoretically linear, in practice, dense insertions and delayed rebalancing degrade its performance on already sorted input.
Execution Time for Descending Sorted Inputs
Descending Sorted Inputs
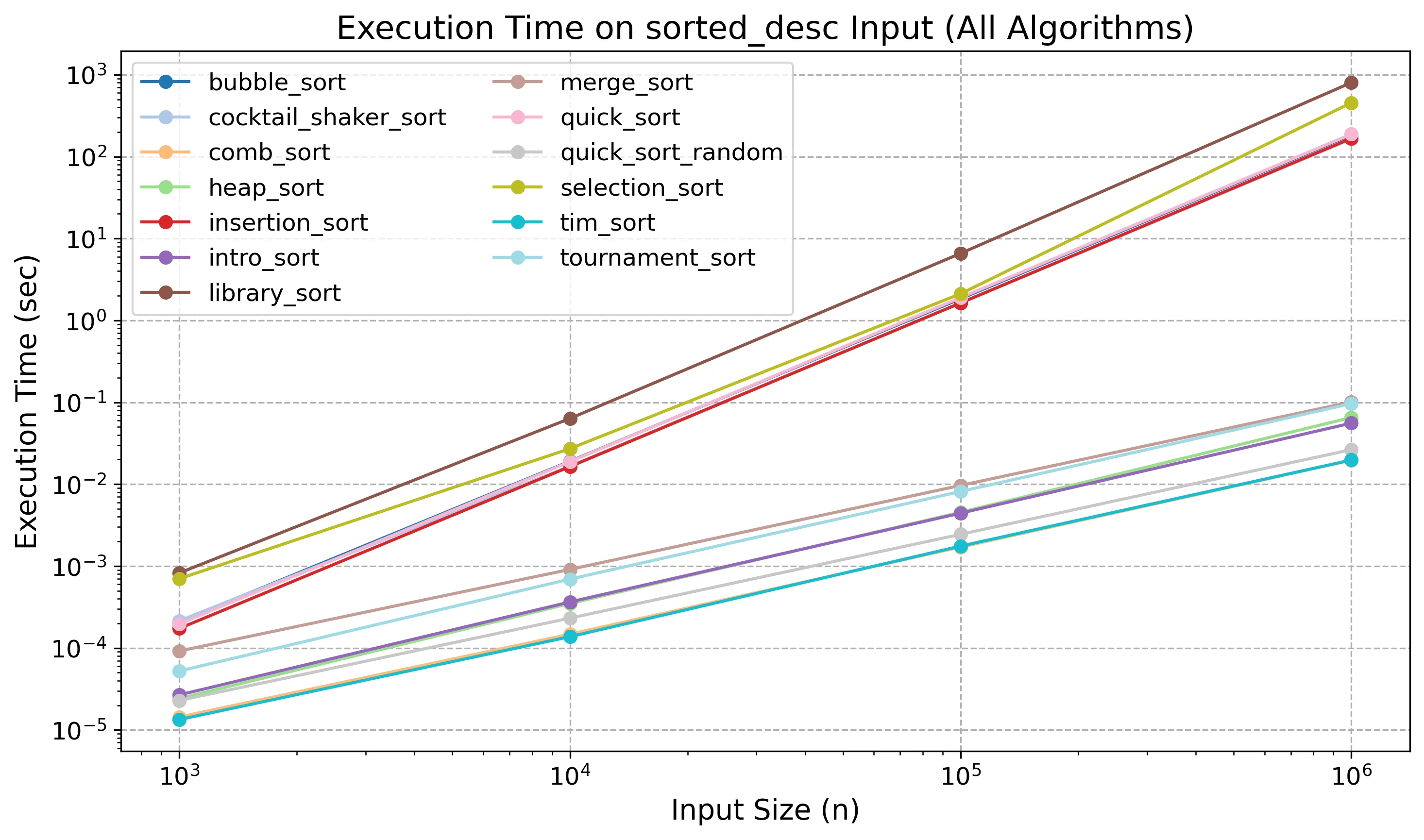
When input is sorted in descending order, many algorithms hit their worst-case behavior:
-
Insertion Sort shows a massive performance drop. Every new element must be shifted across the sorted portion, resulting in O(n²) time. In measurements, latency increased by over 400× compared to the ascending case.
-
Bubble Sort also reaches worst-case performance, with no early exit possible. All elements are compared and swapped.
-
Quick Sort (with fixed pivot) performs poorly again. Descending input leads to highly unbalanced partitions and deep recursion, nearly doubling the runtime compared to random input.
-
Tim Sort, however, remains robust. It detects the long descending runs and reverses them efficiently, maintaining similar performance to the ascending case.
Performance Sensitivity to Data Type
Method Each algorithm was benchmarked on arrays of size n = 10⁶, using the same values cast into four types:
intlong longfloatdouble
All values were sampled uniformly from [0, 10⁶). This isolates the effect of data representation and eliminates rounding issues.
Latency by Data Type for 10⁶ Random Inputs (in seconds)
| Algorithm | int | long long | float | double |
|---|---|---|---|---|
| Merge Sort | 0.1052s | 0.1172s | 0.1288s | 0.1405s |
| Heap Sort | 0.0817s | 0.0900s | 0.1005s | 0.1064s |
| Bubble Sort | 921.3660s | 926.2290s | 1113.9800s | 1127.9900s |
| Insertion Sort | 72.1336s | 77.4562s | 74.7377s | 81.7258s |
| Selection Sort* | 175.8300s | 232.0120s | 245.9670s | 293.1080s |
| Quick Sort | 0.0534s | 0.0526s | 0.0650s | 0.0652s |
| Quick Sort (Random) | 0.0584s | 0.0581s | 0.0703s | 0.0706s |
| Library Sort | 0.1384s | 0.1528s | 0.1607s | 0.1808s |
| Cocktail Shaker Sort | 560.8050s | 562.9870s | 683.0070s | 702.3440s |
| Tim Sort | 0.0403s | 0.0442s | 0.0638s | 0.0667s |
| Comb Sort | 0.0760s | 0.0759s | 0.0913s | 0.0927s |
| Tournament Sort* | 0.2014s | 0.2679s | 0.2511s | 0.4492s |
| Intro Sort | 0.0492s | 0.0494s | 0.0611s | 0.0615s |
Impact of Numeric Type on Sorting Performance
-
Integer bit-width (int vs long long) Performance difference is minimal. Sorting latency barely changes even though
long longis 64-bit. -
Floating-point types (float, double) Introduce consistent slowdowns across all algorithms. Causes:
- Floating-point comparisons are slower due to hardware design
- Arithmetic requires normalization, rounding, precision logic
- Memory footprint increases, impacting cache locality and vectorization
-
Surprisingly,
doubledoes not perform significantly worse thanfloat, suggesting that control-path overhead dominates over raw data size. -
Algorithms like Selection Sort and Tournament Sort are more affected, as they perform many value movements or full-width tree updates. In those cases, memory movement dominates the runtime cost.
Exceptions: Bit-Width as a Bottleneck in Select Algorithms
While most sorting algorithms are bottlenecked by the number of comparisons, a few are particularly sensitive to data size due to the frequency of element movement:
-
Selection Sort performs O(n²) swaps. As the element width increases, memory traffic and cache pressure intensify, leading to performance degradation.
-
Tournament Sort maintains a binary tree of approximately 2n full-width nodes. Wider element types significantly increase memory transfer overhead, making the sort more bound by data movement than pure computation.
Stability Analysis
To assess sorting stability, each algorithm was tested on 1,000 random (value, index) pairs. The values were drawn from the range [0, 50) and had duplicate values but unique original indices. Each algorithm was run 10 times and marked Stable only if it preserved the relative order of equal elements in all runs.
Stability Results
| Algorithm | Stability | Algorithm | Stability |
|---|---|---|---|
| Merge Sort | Stable | Library Sort | Unstable |
| Heap Sort | Unstable | Cocktail Shaker Sort | Stable |
| Bubble Sort | Stable | Tim Sort | Stable |
| Insertion Sort | Stable | Comb Sort | Unstable |
| Selection Sort | Unstable | Tournament Sort | Stable* |
| Quick Sort | Unstable | Intro Sort | Unstable |
Stable Algorithms
- Merge Sort, Insertion Sort, Bubble Sort, Cocktail Shaker Sort, and Tim Sort consistently preserved the relative order of equal elements.
Unstable Algorithms
- Heap Sort, Selection Sort, Quick Sort, Library Sort, Comb Sort, and Intro Sort all exhibited instability.
- The primary cause is element-swapping logic or partitioning steps that do not respect the original order of equal elements.
Special Case: Tournament Sort
- Tournament Sort was stable in our implementation.
- However, its behavior depends on how tie-breaking between equal elements is handled.
- Since
std::min(or similar min logic) does not guarantee consistent results for equal inputs, we explicitly enforced left-child priority to ensure consistent output order.
Memory Usage Across Algorithms
Method Each algorithm was tested on a randomly generated input of size n = 10⁵ using int arrays. Memory usage was sampled at three key points:
- Before loading the input
- After loading the input into a
std::vector - At peak during sorting
We define:
- vector_only = memory after loading vector − memory before loading
- sort_overhead = peak memory during sort − memory after vector load
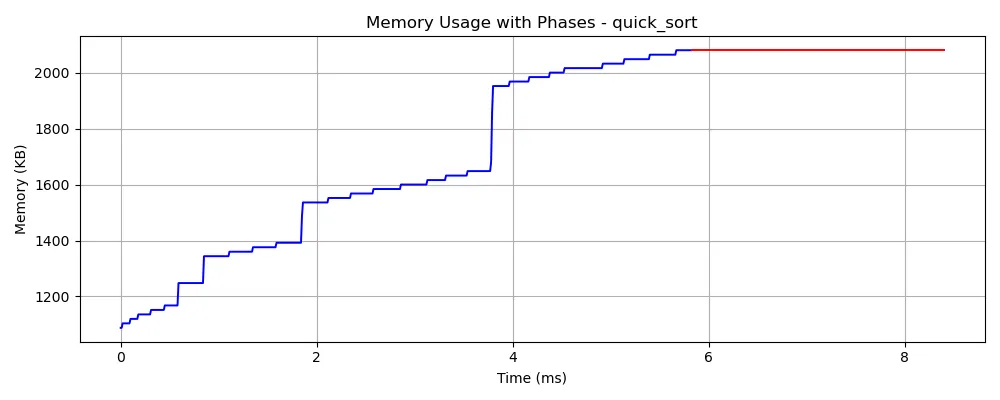
In visualizations, blue indicates memory used for std::vector, and red shows memory fluctuation during sorting.
Memory Usage (KB) for n = 10⁵ Inputs
| Algorithm | Vector Only (KB) | Sort Overhead (KB) |
|---|---|---|
| Merge Sort | 1043.2 | 947.2 |
| Heap Sort | 1024.0 | 0.0 |
| Bubble Sort | 1028.8 | 0.0 |
| Insertion Sort | 1014.4 | 0.0 |
| Selection Sort | 1017.6 | 0.0 |
| Quick Sort | 1020.8 | 0.0 |
| Quick Sort (Random) | 1022.4 | 0.0 |
| Library Sort | 1017.6 | 2601.6 |
| Tim Sort | 1024.0 | 476.8 |
| Cocktail Shaker Sort | 1014.4 | 0.0 |
| Comb Sort | 1011.2 | 0.0 |
| Tournament Sort | 1011.2 | 1454.4 |
| Intro Sort | 1020.8 | 0.0 |
In-Place Sorting Verification
The vector_only values (~1010–1040 KB) reflect memory used by 100,000-element integer vectors. The following algorithms reported 0 KB overhead, confirming they are truly in-place:
- Bubble Sort
- Insertion Sort
- Selection Sort
- Heap Sort
- Quick Sort (including random pivot)
- Comb Sort
- Cocktail Shaker Sort
- Intro Sort
Expected Linear Overheads
- Merge Sort used ~947 KB extra memory, consistent with its auxiliary array size (same as input).
- Tim Sort added ~477 KB. As a hybrid of Insertion and Merge Sort, this overhead comes from temporary buffers used to merge runs — though not the entire array at once.
- Tournament Sort showed ~1.45 MB of overhead. This is expected: it stores both internal nodes and leaves in a binary tree structure, effectively doubling input size.
Memory Growth Pattern in Library Sort
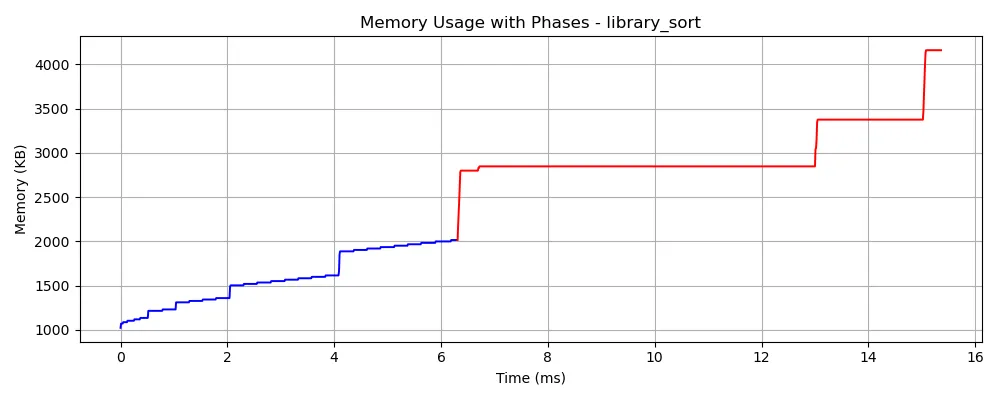
🟦 Blue region: std::vector memory
🟥 Red region: temporary buffers, recursion stacks, trees, etc.
📉 Memory-efficient: Quick/Heap/Insertion
📈 Heavy-memory: Merge/Library/Tournament Sort
As shown in the memory trace figure, Library Sort exhibits four distinct memory spikes during execution. These correspond to repeated reallocations caused by gap exhaustion — when the current array fills up:
- Each spike marks allocation of a larger array and full copy of elements.
- The final spike likely results from compaction or copying of the final output.
- This behavior reflects the algorithm’s reliance on partially filled arrays and rebalancing, which introduce overhead not seen in strictly in-place algorithms.
Accuracy Analysis
Method Accuracy was measured using the adjacent pair violation rate:
\[\text{Accuracy} = 1 - \frac{\# \text{ of violations where } A[i] > A[i+1]}{n - 1}\]For a perfectly sorted array, the violation count is 0, yielding 100% accuracy. We evaluated this metric alongside runtime across various input types and sizes.
Accuracy and Runtime of Library Sort
| Size | Input Type | Time (s) | Accuracy (%) |
|---|---|---|---|
| 10³ | partial_50 | 0.000406 | 99.20 |
| 10³ | random | 0.000072 | 98.80 |
| 10³ | sorted_asc | 0.001195 | 100.00 |
| 10³ | sorted_desc | 0.000826 | 100.00 |
| 10⁴ | partial_50 | 0.026388 | 99.24 |
| 10⁴ | random | 0.000825 | 99.57 |
| 10⁴ | sorted_asc | 0.102631 | 100.00 |
| 10⁴ | sorted_desc | 0.063526 | 100.00 |
| 10⁵ | partial_50 | 2.538908 | 99.31 |
| 10⁵ | random | 0.012318 | 99.27 |
| 10⁵ | sorted_asc | 9.880547 | 100.00 |
| 10⁵ | sorted_desc | 6.584756 | 100.00 |
| 10⁶ | partial_50 | 289.247667 | 99.02 |
| 10⁶ | random | 0.138682 | 99.13 |
| 10⁶ | sorted_asc | 1175.510000 | 100.00 |
| 10⁶ | sorted_desc | 801.178000 | 100.00 |
Overall Accuracy Result
✅ All algorithms except Library Sort achieved 100% accuracy on all test cases.
⚠️ Library Sort showed minor accuracy loss (typically < 1%) on random and partially sorted inputs.
Error Characteristics of Library Sort
- Minor violations arise not from global misordering but local adjacent inversions left unresolved.
-
These typically result from:
- Long rightward shifts during dense insertions
- Deferred or incomplete rebalancing steps
- When insertion density is high near the end and no final rebalance occurs, a few adjacent out-of-order pairs may remain.
Perfect Accuracy on Sorted Inputs
On fully sorted inputs (ascending or descending):
- Every element is inserted without shifting or rebalance
- No local disorder is introduced
- Result: 100% adjacent pair accuracy with zero violations
💬 Thoughts
What I enjoyed most about the sorting algorithm project was seeing just how many different ways there are to solve what seems like the same problem. There’s no “best” sorting algorithm — each one has its strengths depending on the situation, whether it’s input size, distribution, or memory constraints.
It was also fascinating to realize that even something as old and “solved” as sorting is still an active area of research, with ideas like hybrid sorting (e.g. TimSort) used in modern languages like C++ and Python. I used to take built-in sort functions for granted, but now I see the layers of design behind them.
Studying lesser-known algorithms like Library Sort through actual papers was honestly hard — especially figuring out the rebalancing logic — but that made it more satisfying. It wasn’t just copy-pasting theory; I had to implement, debug, and understand the weird edge cases on my own.
Also, using Overleaf for the first time felt like writing a real paper — start to finish, with figures, tables, and everything. That gave me a strong sense of completion, way more than a normal homework writeup.
In the end, this project reminded me that even for problems we “understand,” there’s still depth left to explore — and solving them well still takes engineering, not just theory.
💬 느낀 점
이번 정렬 알고리즘 프로젝트에서 가장 재밌었던 건, 같은 정렬 문제라도 알고리즘이 정말 다양하다는 점이었다. 무조건 빠른 게 좋은 게 아니라, 상황(데이터 분포, 메모리 제약, 입력 크기 등)에 따라 각각 장단점이 다르다는 게 신기했다.
또, 정렬처럼 고전적이고 “이미 다 연구된 것 같은 주제”에도 아직까지 하이브리드 알고리즘처럼 새로운 시도들이 이어지고 있다는 사실이 놀라웠다. C++이나 Python 표준 라이브러리에 들어 있는 TimSort도 이번에 처음 제대로 원리를 알게 되었고, 그동안은 그냥 .sort() 써도 당연한 걸로 생각했는데, 그 안에도 수많은 최적화가 있다는 걸 깨달았다.
Library Sort 같이 잘 알려지지 않은 알고리즘은 논문 보고 구현하는 게 진짜 어려웠다. 갭 재배치 로직 같은 건 디버깅하면서 이해해야 했고, 중간에 잘못된 구현 때문에 정확도도 낮게 나와서 엄청 고생했다. 그래도 내가 직접 논문 보고 구현하고, 논문처럼 작성해서 정리한 과정 자체가 뿌듯했다.
Overleaf 처음 써봤는데, 그냥 과제하는 느낌이 아니라 진짜 논문 쓰는 느낌이라 완성하고 나니까 성취감도 훨씬 컸다.
정렬이라는 익숙한 문제도 파고들다 보면 결국 이론 + 구현 + 최적화가 다 들어가는 종합 문제라는 걸 다시 느꼈다. 단순히 정답만 구하는 게 아니라, 조건에 따라 좋은 선택을 하는 것 자체가 알고리즘 설계라는 걸 배운 것 같다.