TSP Algorithm
Implements and evaluates classical and novel algorithms for the Traveling Salesman Problem, with a focus on flow-based cycle covers and local refinements.
📄 PDF: Project PDF
INTRODUCTION
The Traveling Salesman Problem (TSP) is a well-known NP-hard problem in combinatorial optimization. It seeks the shortest tour that visits each city exactly once and returns to the origin, with applications ranging from logistics to circuit design.
To address its computational intractability, a wide range of heuristics and approximation algorithms have been developed. The MST-based 2-approximation algorithm provides theoretical guarantees under the triangle inequality, while greedy and local search methods such as 2-opt offer strong empirical performance despite lacking worst-case bounds.
In this project, we implement several classical algorithms including Held-Karp dynamic programming, MST-based approximation, greedy heuristics, and 2-opt refinement, as well as a novel flow-based heuristic. This method leverages minimum-cost maximum-flow (MCMF) to generate cycle covers, which are then refined by 2-opt. We also apply k-nearest-neighbor sparsification to improve scalability.
Although our method is generally slower than classical heuristics, its combination with 2-opt yields comparable tour quality. Sparsification significantly reduces runtime, making the approach more practical for larger instances.
PROBLEM STATEMENT
The Traveling Salesman Problem (TSP) asks: given a set of n cities and pairwise costs c₍ᵢⱼ₎, find the shortest possible tour that visits each city exactly once and returns to the starting point. Formally, for V = {v₁, v₂, …, vₙ}, the objective is:
min over π ∈ Sₙ of ( c[π(n)][π(1)] + ∑ᵢ₌₁ⁿ⁻¹ c[π(i)][π(i+1)] )
where Sₙ is the set of all permutations of n elements.
Computational Complexity
TSP is a classic NP-hard problem. The decision version is NP-complete, and the optimization version is NP-hard but not known to be in NP. Since the number of feasible tours grows factorially, exact algorithms quickly become infeasible as n increases.
Approximation Motivation
Due to the problem’s intractability, various approximation algorithms have been proposed for the metric TSP. MST-based methods offer theoretical guarantees, while Greedy and 2-opt heuristics perform well in practice. Our method builds on these ideas by combining global flow structure with local refinement.
EXISTING ALGORITHMS
Held-Karp (Dynamic Programming)
The Held-Karp algorithm [Held & Karp, 1962] computes the exact TSP solution via dynamic programming by storing the minimal cost C(S, j) of reaching city j through subset S. It avoids enumerating all n! permutations by using the recurrence:
C(S, j) = min over k ∈ S \ {j} of [ C(S \ {j}, k) + c_kj ]
with base case:
C({1, j}, j) = c_1j
Assuming city 1 is the start, the optimal tour cost is:
min over j ≠ 1 of [ C({1,...,n}, j) + c_j1 ]
Pseudocode: Held-Karp-TSP
\begin{algorithm}
\caption{Held-Karp TSP}
\begin{algorithmic}
\FOR{$j := 2$ \TO $n$}
\STATE $C[\{1,j\}][j] := c_{1j}$
\ENDFOR
\FOR{$s := 3$ \TO $n$}
\FOR{each $S$ of size $s$ containing $1$}
\FOR{$j \in S \setminus \{1\}$}
\STATE $C[S][j] := \min_k \left(C[S \setminus \{j\}][k] + c_{kj}\right)$
\ENDFOR
\ENDFOR
\ENDFOR
\STATE Reconstruct tour $T$ from $C$
\RETURN $T$
\end{algorithmic}
\end{algorithm}
Time and Space Complexity
- Time: 𝒪(n² · 2ⁿ)
- Space: 𝒪(n · 2ⁿ)
Advantages
- Provides the exact optimal solution for small instances.
Limitations
- Exponential time and space complexity makes it infeasible beyond n > 30
- Generally superseded by efficient solvers like Concorde.
MST-based 2-Approximation Algorithm
This classical algorithm [CLRS 3rd ed.] constructs a tour with cost at most twice the optimal, assuming the triangle inequality. It builds a Minimum Spanning Tree (MST), performs a preorder traversal to list the nodes, and shortcuts repeated visits to yield a Hamiltonian tour.
Pseudocode: MST-Based-TSP
\begin{algorithm}
\caption{MST-Based TSP}
\begin{algorithmic}
\STATE choose start node r
\STATE compute MST T rooted at r (e.g., Prim’s algorithm)
\STATE perform preorder traversal on T to obtain path P
\STATE shortcut repeated nodes in P to construct Hamiltonian tour H
\RETURN tour H
\end{algorithmic}
\end{algorithm}
Time and Space Complexity
- Time: 𝒪(n²)
- Space: 𝒪(n)
Approximation Guarantee
Let H* be the optimal tour and T the MST. Then:
-
Removing one edge from H* yields a spanning tree ⇒ → c(T) ≤ c(H*)
-
A DFS traversal of T visits each edge twice ⇒ → c(W) = 2 · c(T) ≤ 2 · c(H*)
-
Using the triangle inequality, shortcutting repeated nodes gives a tour H such that:
c(H) ≤ c(W) ≤ 2 · c(H*)
Thus, the output tour is guaranteed to be at most twice the cost of the optimal solution. This algorithm is a formal 2-approximation for the metric TSP.
Advantages
- Simple and easy to implement
- Offers a provable 2-approximation guarantee under the triangle inequality
Limitations
- In the worst case, it may return a tour nearly twice as long as optimal
- The approximation guarantee fails if the triangle inequality does not hold
Greedy Nearest-Neighbor Heuristic
This heuristic, originally introduced by Flood [1956], builds a tour by repeatedly visiting the closest unvisited city. Starting from an initial node, it adds the nearest neighbor to the tour until all cities are visited, then returns to the starting city to complete the tour.
Pseudocode: Greedy-TSP
\begin{algorithm}
\caption{Greedy TSP}
\begin{algorithmic}
\STATE tour := [v0], visited := \{v0\}
\WHILE{some cities remain unvisited}
\STATE let u be the nearest unvisited neighbor of last node in tour
\STATE append u to tour
\STATE mark u as visited
\ENDWHILE
\STATE append v0 to close the tour
\RETURN tour
\end{algorithmic}
\end{algorithm}
Time and Space Complexity
- Time: 𝒪(n²)
- Space: 𝒪(n)
Approximation Behavior
Despite its simplicity, Greedy offers no worst-case or approximation guarantee, and may produce tours arbitrarily worse than optimal. However:
- It performs well on Euclidean or spatially clustered data
- Often outperforms MST-based tours in practice
- Recent work by Frieze and Pegden (2024) shows that its average-case performance is significantly better than worst-case expectations
Advantages
- Extremely fast
- Easy to implement
- Performs well on spatial or metric inputs
Limitations
- No global planning → can perform poorly in adversarial/non-metric cases
2-Opt Local Optimization
2-opt [Croes, 1958] improves a tour by iteratively swapping two edges to reduce total cost. It is commonly used for post-processing heuristic tours.
Pseudocode: Two-Opt
while any 2-swap improves cost:
check all pairs of non-adjacent edges
if a swap improves the tour:
apply the swap
return improved tour
Time and Space Complexity
-
Time: 𝒪(k · n²), where
- k = O(1) for structured inputs
- k = O(n) for random inputs
-
Space: 𝒪(n)
So, total time ranges from 𝒪(n²) to 𝒪(n³) depending on input structure.
Advantages
- Highly effective local optimization
- Consistently improves tour quality
Limitations
- Can converge to local optima
- May be slow if applied to poor initial tours
Table: Comparison between base and +2opt variants across datasets
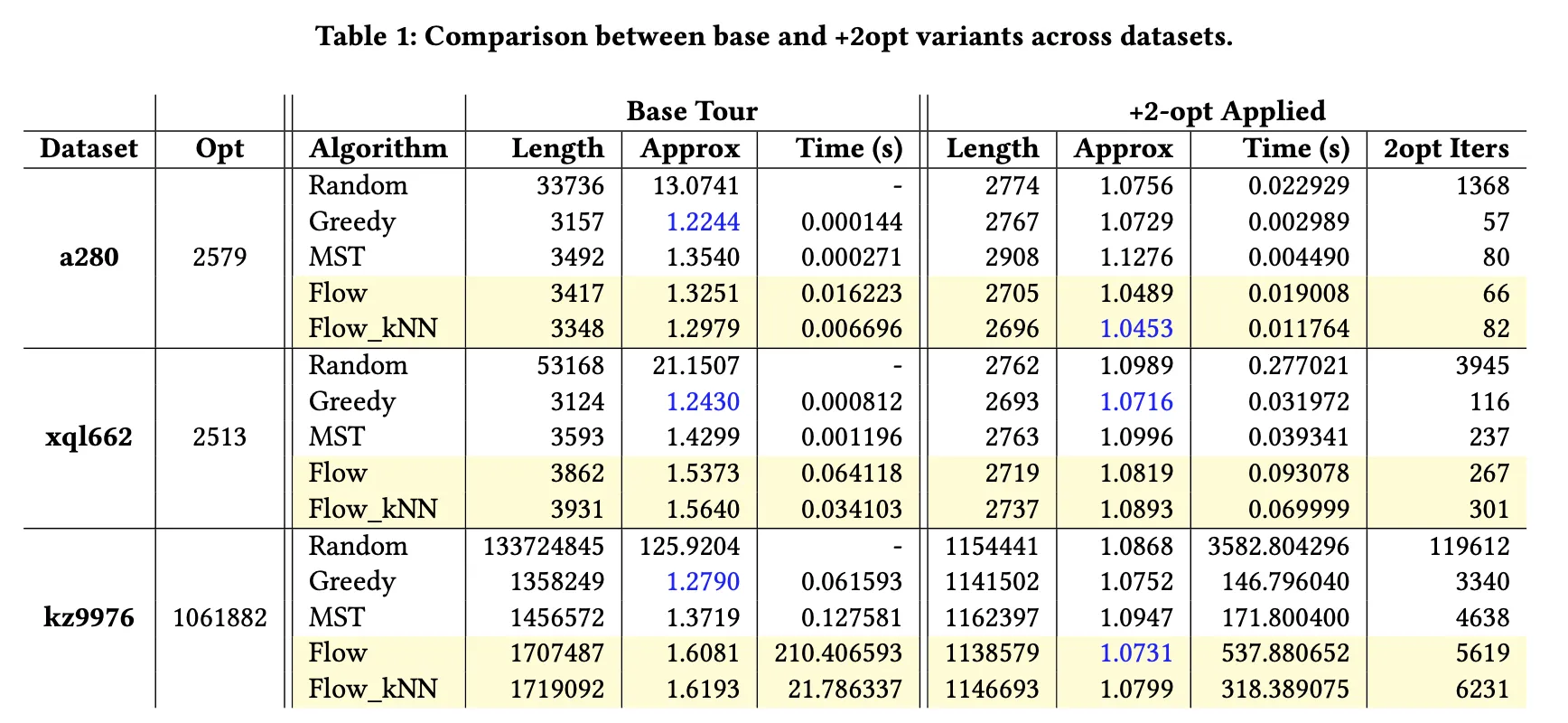
| Dataset | Opt | Algorithm | Base Length | Base Approx | Base Time (s) | +2opt Length | +2opt Approx | +2opt Time (s) | 2opt Iters |
|---|---|---|---|---|---|---|---|---|---|
| a280 | 2579 | Random | 33736 | 13.0741 | - | 2774 | 1.0756 | 0.0229 | 1368 |
| Greedy | 3157 | 1.2244 | 0.0001 | 2767 | 1.0729 | 0.0030 | 57 | ||
| MST | 3492 | 1.3540 | 0.0003 | 2908 | 1.1276 | 0.0045 | 80 | ||
| Flow | 3417 | 1.3251 | 0.0162 | 2705 | 1.0489 | 0.0190 | 66 | ||
| Flow_kNN | 3348 | 1.2979 | 0.0067 | 2696 | 1.0453 | 0.0118 | 82 | ||
| xql662 | 2513 | Random | 53168 | 21.1507 | - | 2762 | 1.0989 | 0.2770 | 3945 |
| Greedy | 3124 | 1.2430 | 0.0008 | 2693 | 1.0716 | 0.0320 | 116 | ||
| MST | 3593 | 1.4299 | 0.0012 | 2763 | 1.0996 | 0.0393 | 237 | ||
| Flow | 3862 | 1.5373 | 0.0641 | 2719 | 1.0819 | 0.0931 | 267 | ||
| Flow_kNN | 3931 | 1.5640 | 0.0341 | 2737 | 1.0893 | 0.0700 | 301 | ||
| kz9976 | 1061882 | Random | 133724845 | 125.9204 | - | 1154441 | 1.0868 | 3582.8043 | 119612 |
| Greedy | 1358249 | 1.2790 | 0.0616 | 1141502 | 1.0752 | 146.7960 | 3340 | ||
| MST | 1456572 | 1.3719 | 0.1276 | 1162397 | 1.0947 | 171.8004 | 4638 | ||
| Flow | 1707487 | 1.6081 | 210.4066 | 1138579 | 1.0731 | 537.8807 | 5619 | ||
| Flow_kNN | 1719092 | 1.6193 | 21.7863 | 1146693 | 1.0799 | 318.3891 | 6231 |
PROPOSED ALGORITHM
Existing heuristics like Greedy and MST tend to focus on local optimization and may miss global structure. We adopt Minimum-Cost Maximum-Flow (MCMF) to better capture global cost patterns by generating a one-to-one matching across the entire set of cities. To compensate for the potential loss of local structure, we enhance the solution with Greedy-like subtour merging and 2-opt refinement.
Flow-based Cycle Cover via MCMF
We model the TSP as a cycle cover problem. The idea is to:
- Construct a bipartite flow graph with two copies of the city set.
- Apply MCMF to find a minimum-cost one-to-one assignment.
- Extract disjoint subtours (cycles).
- Iteratively merge cycles using the closest-pair heuristic.
Pseudocode: Flow-Cycle-Cover-TSP
Construct bipartite graph with source s, sink t, and city sets L and R
Connect s → Lᵢ and Rⱼ → t with capacity 1 and cost 0
Connect Lᵢ → Rⱼ with capacity 1 and cost cᵢⱼ for all i ≠ j
Run MCMF from s to t to obtain flow-based matching
Extract subtours from flow result
while more than one subtour remains:
merge the two closest subtours
return final merged tour T
Time and Space Complexity
Using SPFA for shortest paths:
- Time: 𝒪(n³)
- Space: 𝒪(n²)
kNN Sparsification for Scalability
To improve efficiency, we retain only the k-nearest neighbors per node when constructing the bipartite graph. This sparsification:
- Reduces edge count
- Preserves local structure
- Retains most of MCMF’s matching quality
Time and Space Complexity
- Time: 𝒪(kn²)
- Space: 𝒪(kn)
- In practice: k = 20
Refinement with 2-opt
After merging cycles from MCMF, the resulting tour may contain:
- Long edges
- Suboptimal transitions
- Edge crossings
To refine this, we apply 2-opt, which:
- Eliminates crossings
- Replaces long edges
- Improves tour quality locally
Summary
By combining:
- Global optimization via MCMF
- Graph sparsification with kNN
- Local refinement using 2-opt
we achieve a hybrid algorithm that balances solution quality and computational cost.
EXPERIMENTS
Experimental Setup
All experiments were conducted on a MacMini (Apple M4, 16GB RAM). Code was compiled using clang++ with flags -std=c++17 and -O2. Five datasets using the EUC_2D metric were tested:
- weird20.tsp (20 cities)
- a280.tsp (280 cities) Source
- xql662.tsp (662 cities) Source
- kz9976.tsp (9,976 cities) Source
- mona_lisa100K.tsp (100,000 cities) Source
Runtime Comparison
Runtime is primarily dictated by two components:
- The cost of constructing the initial tour
- The cost of refining it with 2-opt
| Algorithm | Notes |
|---|---|
| Greedy | Fastest, runs in milliseconds thanks to nearest-neighbor logic |
| MST | Slightly slower than Greedy but remains efficient |
| Flow-based (Full) | Significantly slower; solving MCMF dominates runtime, especially for large instances |
| Flow-based (kNN) | Improved over Full Flow, but still slower than Greedy or MST |
| 2-opt | Runtime depends heavily on initial structure; more iterations needed when starting from Flow-based subtours |
Solution Quality
Before 2-opt
- Greedy outperforms other heuristics in raw tour quality
- MST has a formal 2-approximation guarantee but often yields longer tours due to tree detours
- Flow / Flow_kNN perform poorly initially due to short, fragmented subtours
After 2-opt
- Greedy improves modestly — already starts near local optimum
- MST gains slight improvement, but some suboptimal edges remain
- Flow / Flow_kNN show the largest improvements, surpassing MST and approaching Greedy’s final tour quality
- Their gains are attributed to low-quality initial solutions, which offer more opportunity for refinement
Observations on MCMF Initialization
- MCMF often yields many short subtours, especially 2-cycles
- This disrupts the intended global matching behavior
- The algorithm relies heavily on 2-opt to recover a valid tour
- This increases both the number of iterations and the total runtime
In summary, Flow-based methods benefit most from post-processing but are computationally expensive. Greedy remains the best trade-off for performance vs. quality.
Ablation: Flow-based Cycle Cover Variants
Table highlights how $k$NN sparsification significantly reduces the number of edges processed during the MCMF step, resulting in noticeable runtime improvements. In particular, Flow_kNN demonstrates superior scalability compared to the full Flow method, especially on large-scale datasets such as kz9976 and mona_lisa100K.
Visual Comparison Before and After 2-opt Refinement
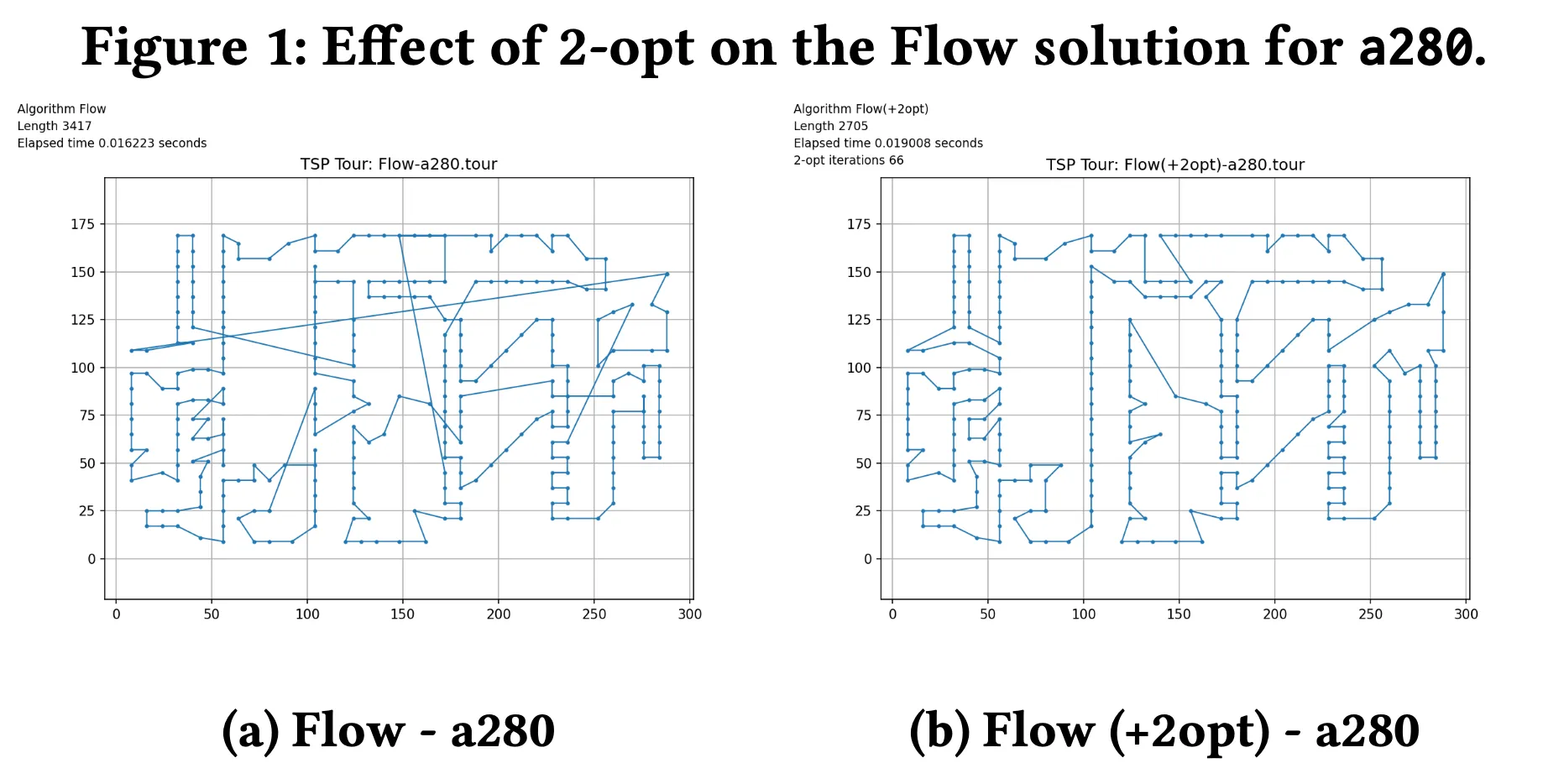
Figure: Effect of 2-opt on the Flow-based tour for a280.
In the initial Flow-generated tour, many long cross-edges are present, resulting from the greedy subtour merging phase. The application of 2-opt significantly improves this, by identifying and replacing suboptimal segments, leading to:
- More compact routing
- Fewer long edges
- Lower total cost
This is clearly reflected in the post-2opt diagram, where the path appears more coherent and globally efficient.
Final Observation
Both kNN sparsification and 2-opt operate in $\mathcal{O}(n^2)$ time, and when used together, they produce:
- Near-optimal tours
- Significantly lower memory and runtime cost than full-flow matching
- High scalability to tens of thousands of cities
We conclude that Flow_kNN + 2-opt is a practical and effective hybrid strategy that balances global planning with local refinement.
Additional Results
To test performance at both ends of the scale, we evaluated a tiny instance (weird20) and a massive dataset (mona_lisa100K). Results are shown in Table~\ref{tab:extreme_cases}.
Table: Held-Karp and Large-scale Results
| Dataset | Algorithm | Length | Time (s) |
|---|---|---|---|
weird20 | Held-Karp | 439 | 43.25 |
mona_lisa100K | Best-known | 5,757,191 | — |
| Greedy | 6,846,598 | 16.99 | |
| MST | 8,394,831 | 32.03 | |
| Flow_kNN | 7,276,478 | 35,205.36 |
Best-known tour: mona_lisa_5757191.tour
weird20 (20 cities)
- Held-Karp gives exact optimal tour in 43 seconds.
- It is feasible only for small instances due to $\mathcal{O}(n^2 2^n)$ complexity.
- Serves as a reference baseline for solution quality.
mona_lisa100K (100,000 cities)
- Greedy yields decent quality with the fastest runtime (17s).
- MST takes longer and produces a much worse tour due to detours.
- Flow_kNN offers better tour quality than MST, at a high computational cost (≈ 10 hours).
Visual Comparison: Flow_kNN vs MST Tours
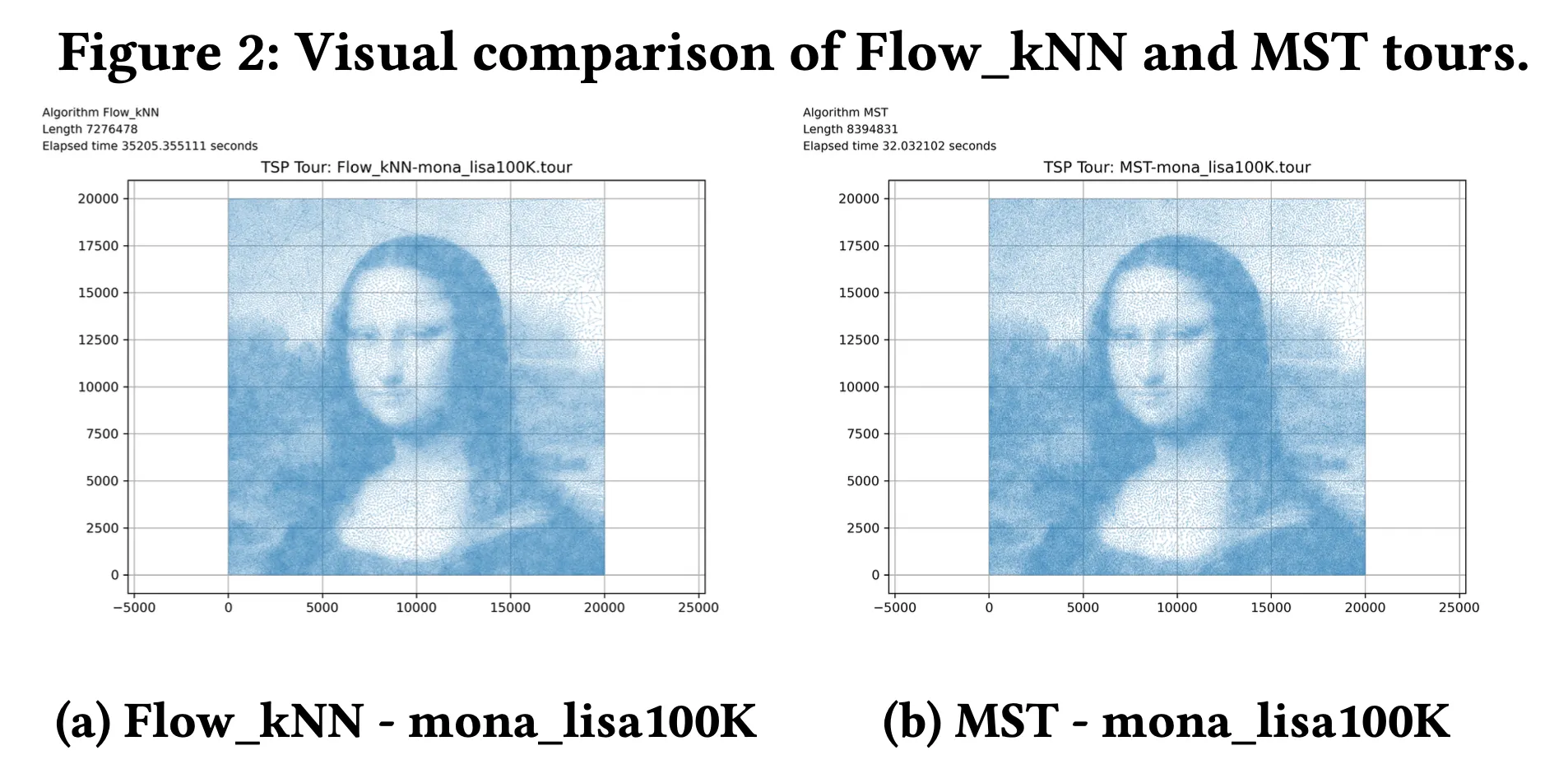
Figure: Comparison of Flow_kNN and MST tours on mona_lisa100K.
Observations
-
Flow_kNN:
- A few long edges (due to early subtour merging)
- Mostly short, coherent connections
- Leads to lower total tour cost
-
MST:
- More uniform edge spacing
- Suffers from accumulated detours, especially in sparse regions
Interestingly, this reverses earlier trends—in smaller datasets, MST often outperforms Flow. But at large scale, global initialization (Flow) appears to become more valuable, suggesting strong potential for Flow-based strategies in high-dimensional TSPs.
CONCLUSION
Summary of Findings This project explored a variety of classical and heuristic algorithms for solving the symmetric Traveling Salesman Problem (TSP). These included:
- Held-Karp dynamic programming for exact solutions,
- MST-based 2-approximation with provable bounds,
- Greedy nearest-neighbor heuristic with strong empirical performance,
- 2-opt local refinement for improving tour quality.
In addition, we proposed a Flow-based Cycle Cover heuristic, which utilizes Minimum-Cost Maximum-Flow (MCMF) to capture global edge structure. We enhanced this approach using $k$-nearest-neighbor sparsification and post-processing with 2-opt.
Performance Analysis Among classical methods, Greedy provided the best balance of speed and quality, often outperforming MST despite its lack of approximation guarantees. The Flow-based method, while theoretically appealing, suffered from fragmented subtours that led to poor initial tours. The majority of its improvements came from 2-opt post-refinement, not from MCMF directly. This suggests that Flow alone is insufficient unless integrated with additional structure-aware mechanisms.
Limitation and Future Work The key weakness of the Flow-based method is its tendency to create short, disjoint cycles, limiting its utility as a standalone solver.
A natural extension is to apply MCMF recursively, where:
- Each subtour is treated as a supernode, and
- A new flow graph is constructed over these aggregates.
However, this raises a new challenge:
- Defining meaningful and consistent inter-subtour distances is difficult.
- Simple metrics (e.g., shortest inter-node edge) often fail to capture structural context and can result in poor merges.
Successfully addressing this would allow purely flow-based, globally coordinated tour construction, offering a new hybrid between combinatorial optimization and network flow methods for large-scale TSPs.
💬 Thoughts
The most fun part of this project was coming up with my own algorithm instead of just using an existing one. I used MCMF to get a global structure and layered 2-opt on top to improve the tour quality — it didn’t feel like I was just solving a homework problem, it actually felt like I was solving a problem.
I always knew TSP was NP-hard, but running an exact algorithm like Held-Karp myself really hit it home. Now I get why people obsess over polynomial time — with exponential time, just increasing the number of cities a bit makes the whole thing blow up. It made me realize why algorithm research actually matters.
At first, I naïvely thought Held-Karp would run fine for something like 200 cities. I let it run, waited… and it never finished. Then I realized 2^200 is an insane number. I even asked GPT if my code had a bug, and it politely roasted me saying there’s no bug — it’s just that even if you had all the computers in the universe, it still wouldn’t finish. That was humbling.
The most surprising part? Problems like Mona Lisa 100K are still being worked on. I thought these had all been solved ages ago, but people are still out there breaking records and trying new ideas. It’s wild and kind of inspiring that there’s still progress being made on such a classic problem.
That said, I wasn’t really happy with my final results. I ran into unexpected issues and had to force 2-opt in just to get something that worked. I didn’t love that, but it was already too late to start over, so I just rolled with it. Still, the project felt different from typical assignments — I got to design something of my own and compare it head-to-head with existing algorithms. That part was really cool.
💬 느낀 점
이번 프로젝트에서 제일 재밌었던 건, 그냥 있는 알고리즘을 쓰는 게 아니라 직접 아이디어 짜서 구현해봤다는 것이다. MCMF로 전체 흐름 잡고, 그 위에 2-opt 붙여서 투어 품질 높이는 방식으로 해봤는데, 단순히 과제 푸는 느낌이 아니라서 재밌었다.
TSP가 NP-hard하다는 건 알고는 있었는데, Held-Karp 같은 정확한 알고리즘을 직접 돌려보니까 깜짝 놀랐다. 왜그렇게 Polynomial Time에 환장하는지 알 것 같다. 지수시간이 되니까 도시 수 조금만 늘어나도 감당 안 되는 걸 보면서 실제로 알고리즘을 왜 연구하는지 느끼게 되었다.
사실 처음에 Held-Karp도 200짜리는 돌아갈줄알고 돌렸는데 안끝나길래 생각해보니까, 2^200은 엄청난 숫자였다. 생각없이 돌리고 GPT한테 코드 오류있냐고 물어봤는데, 오류 없고, 2^200은 우주에 있는 모든 컴퓨터 가져와서 돌려도 안끝난다고 나한테 꼽을 줘서 쪽팔렸다.
제일 인상 깊었던 건, 모나리자 100K처럼 엄청 오래된 TSP 문제들도 아직도 사람들이 더 좋은 해답 찾으려고 노력하고 있다는 것이다. 이미 다 연구됐을 줄 알았는데, 여전히 기록이 깨지고 있다는 게 놀라웠고, 계속 누군가는 노력하는게 멋졌다.
근데 결과가 너무 별로였고, 생각 외의 문제가 발생해서 억지로 2-opt 끼워서 좀 맘에 안들었다. 하지만 도저히 다른 방법을 생각하기에는 늦어서 계속 했던 것 같다. 평범한 과제 느낌이 아니라 나만의 알고리즘을 만들고 이미 존재하는 알고리즘과 성능비교를 해보는게 색달라서 재밌었다.