TTRL: Test-Time Reinforcement Learning
| ArXiv | https://arxiv.org/abs/2504.16084 |
|---|---|
| Github Code | https://github.com/PRIME-RL/TTRL |
| Authors | Yuxin Zuo, Kaiyan Zhang, Li Sheng, Shang Qu, Ganqu Cui, Xuekai Zhu, Haozhan Li, Yuchen Zhang, Xinwei Long, Ermo Hua, Biqing Qi, Youbang Sun, Zhiyuan Ma, Lifan Yuan, Ning Ding, Bowen Zhou |
| Affiliation | Tsinghua University, Shanghai AI Lab |
(1) 다양한 답변을 생성하고 (Test-Time Scaling)
(2) majority voting을 통해 "이 답변은 good, 이건 bad"라는 평가를 자동으로 생성
(3) 이를 reward로 변환해 RL 수행
Test Time에 자율적, 반복적, label-free 방식으로 학습하고 더 좋은 결과를 내는 효과
답안지 안주고 문제만 줬는데, 알아서 반복적으로 문제풀면서 똑똑해진다!
기존의 Test-Time Scaling이나 Reinforcement Learning을 먼저 설명하는게 좋을 것 같아서5 Related Works를 먼저 읽었다.
5 Related Works
5.1 Test-Time Scaling
= LLM이 테스트(추론) 시점에서 더 많은 계산 자원을 사용해 성능을 높이는 방법
→ 즉, 학습된 모델 구조는 그대로 두고, test-time에 inference 방식만 확장하는 전략
① Parallel Generation
하나의 입력에 대해 여러 개의 output을 생성하고 그 중 “좋은 것”을 선택
→ 이처럼 parallel하게 여러 답안을 만들고 하나를 “선택”하거나 “aggregation” 하는 게 공통
② Sequential Generation
하나의 답변을 길게, 점진적으로 확장하거나 수정하며 reasoning
→ reasoning depth를 늘리거나 self-correction을 유도
한계: 대부분의 TTS는 prompt-based이며, 모델 파라미터 자체는 업데이트되지 않음
| 기존 TTS | TTRL |
|---|---|
| inference time에만 사용 | inference + parameter update (TTT) 포함 |
| majority voting만 사용 | majority voting → reward로 전환하여 RL 수행 |
| non-parametric | parametric update 포함 |
5.2 RL for Reasoning
Human Preference 기반
- Human 또는 annotator가 여러 답 중 선호도를 매김
- Preference Model 학습 → reward로 사용
- PPO 등으로 policy (LLM) 업데이트
Rule-based Reward 기반
reasoning domain (예: 수학)에서는 정답을 명확하게 판별할 수 있음
→ 맞았으면 reward = 1, 틀렸으면 0 같은 rule-based reward 사용 가능
GRPO (Group Relative Policy Optimization):
DeepSeek-R1에서 사용. 수학 문제에 대해 긴 CoT 생성 유도
PPO도 사용되지만, 수치적 reward의 안정성과 gradient variance가 문제됨
| 구분 | RLHF | GRPO / Rule-based RL | TTRL |
|---|---|---|---|
| supervision source | human preference | rule-based labels (정답존재) | majority voting (pseudo-label) |
| label 필요 여부 | 필요 | 필요 | 불필요 (label 없음) |
| 학습 시점 | offline RL | offline RL | Test-time (online RL) |
| task | open-domain instruction | math, logic, program | math, logic, program |
2. Test-Time Reinforcement Learning (TTRL)
We study the problem of training a pre-trained model during test time using RL without ground-truth labels. We call this setting Test-Time Reinforcement Learning.
2.1 Methodology
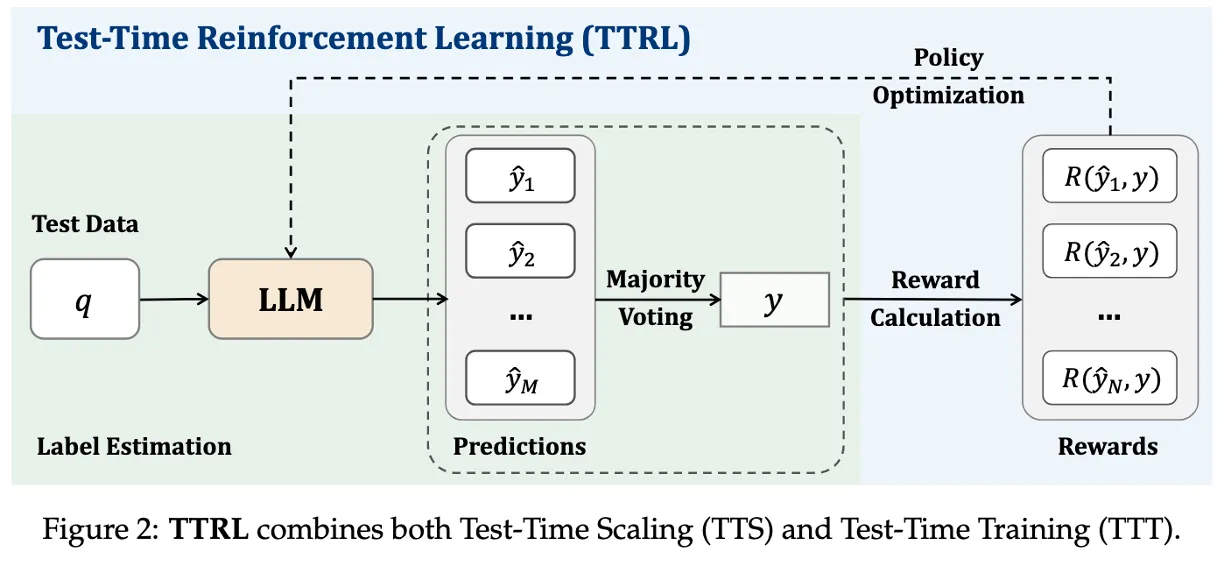
녹색 배경이 TTS + 이후 나온 결과로 reward calaulation을 통해 Test-Time에 Training
M: 한 문제(q)에 대해 생성하는 답변 수
N = batch_size(하나의 학습 step에서 사용하는 문제 수)
첫번째 문제에 M개의 답변 내고, voting하고 reward 계산해서 모아놓은게 R(y1, y)
상태(state)와 행동(action)
→ LLM의 답변 행위 = RL의 action
Rollout: 답변 여러 개 생성
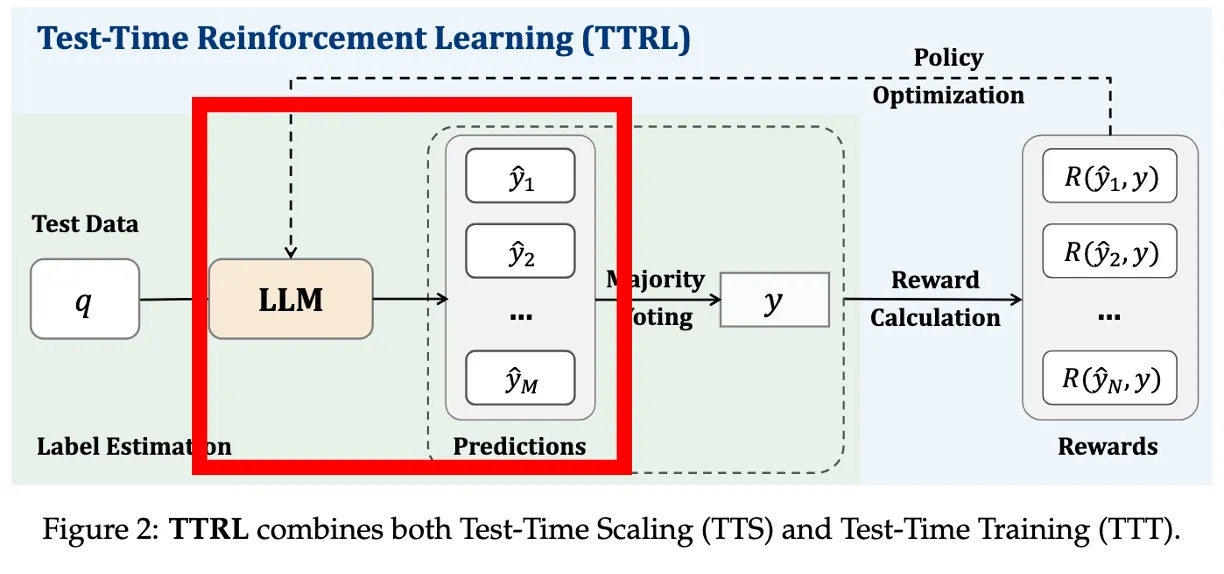
Ground-truth label이 없이 reward signal을 보내야하니까, 여러개의 candidate(후보) output을 생성
→ x에 대해 답변 {y1,...,yM} 을 sampling
랜덤성 있는 샘플링으로 M=64개의 다양한 답변 생성(appendix에서는 16)
→ 단일 답이 아닌 다양한 reasoning path를 확보해야 voting이 의미 있음
여러개의 답변은 자동으로 랜덤되는것인가? 따로 설정을 바꿔주는것인가?
원래 LLM은 같은 입력에 대해서도 랜덤하게 다르게 나오긴 함.
파라미터를 일부러 변화시키진 않고, Randomized decoding 설정
→ temperature, top-p, top-k, sampling 횟수 등으로 조절

temperature = 0.6top-p = 0.95→ sampling된 답변이 다르게 나오도록 유도
Temperature: Setting the temperature to 1.0, as opposed to 0.6, increases the model’s output entropy. This promotes more extensive exploration and allows the model to make better use of its prior knowledge for self-improvement, which is particularly important when addressing challenging benchmarks.
실제로 이후 실험에서 Parameter에 따른 비교가 있고,
Dataset 난이도에 따라서 조정이 필요하다는 한계를 밝힘.
(Figure 11 : Inappropriate RL Hyperparameters)
어려운 task에 대해서는 Temperature을 1.0으로 해야 효과가 좋음.
→ temperature 높이면 diversity 증가 → exploration 증가 → high entropy → 다양한 답변
정답 추출 + Majority Voting (Label 추정)
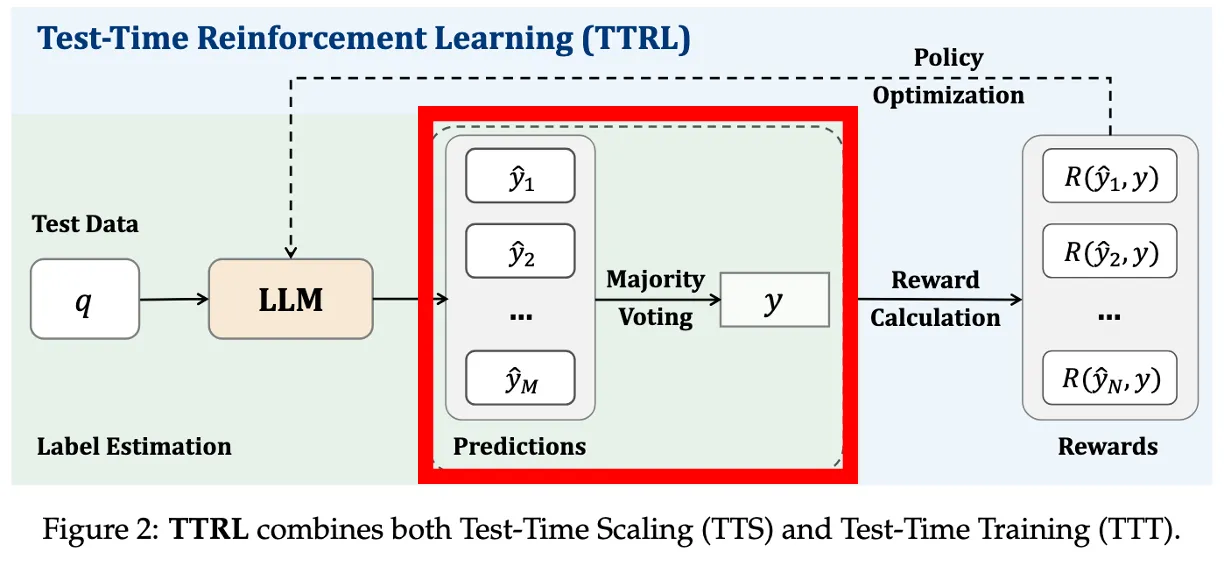
Reward 계산
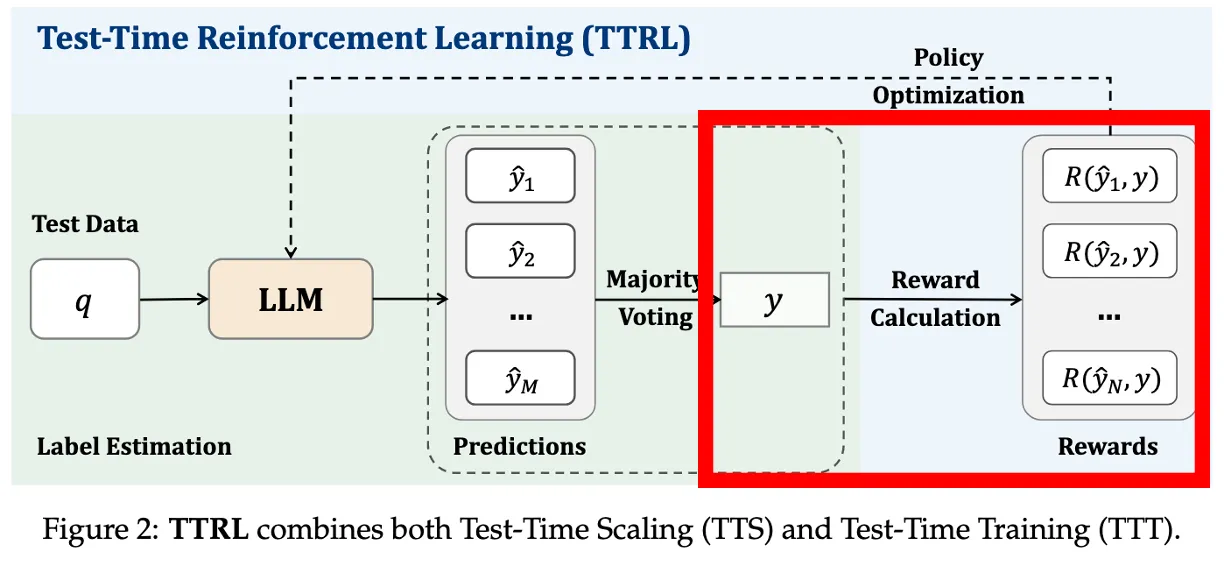
sampling된 y답이 majority 답이랑 일치하면 → reward = 1
아니면 → reward = 0
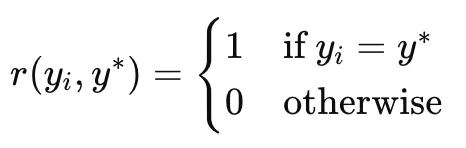
→ 실제 정답을 모르지만, voting 결과에 얼마나 일치했는지를 기준으로 학습 신호 제공
We sample 64 responses per prompt using the current model and randomly select 32 to use for training.
랜덤하게 32개를 트레이닝에 사용그 중 32개만 골라서 reward 계산에 사용
→ 투표는 64개로 하는데, 나중에 RL은 랜덤으로 반만 사용함. (너무 계산 과도하니까)
Each RL step samples a batch of questions and computes policy gradients using the pseudo-rewards from majority voting.→ 각 step마다 여러 개의 질문(batch of questions)을 사용
→ 이게 곧 우리가 말하는 “batch size”에 해당
데이터셋마다 다르게 사용했음.
AIME=80, AMC=30, MATH-500=10
AIME는 어려우니까 여러번하고 업데이트해줘야 틀린 정보로 업데이트가 반복될 확률이 줄어듬.
Policy 업데이트 (RL)
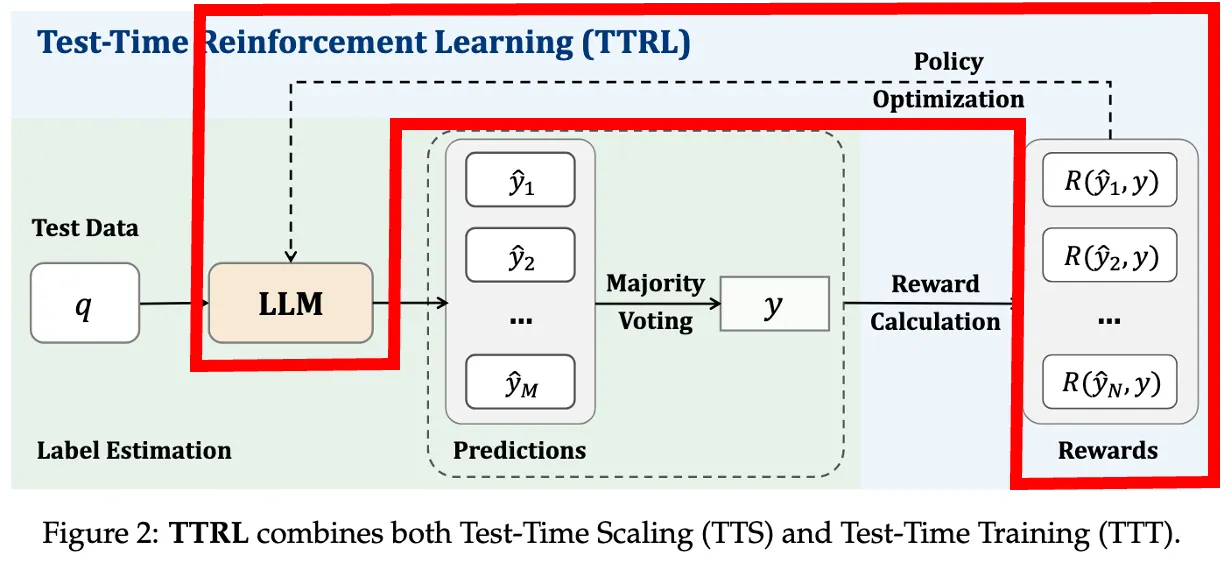
batch size만큼 반복하면 이제 모아놨던
목표: expected reward를 최대화하는 것 → 다수결이 옳다고 믿자!
reward가 높았던 답변 쪽으로 (gradient ascent)
θ (모델 파라미터)를 업데이트
2.2 Majority Voting Reward Function

from collections import Counter
def majority_voting_reward_fn(outputs):
# 1. 정답 추출
answers = [extract_answer(output) for output in outputs]
# 2. 다수결로 label 추정
counts = Counter(answers)
majority_answer, _ = counts.most_common(1)[0]
# 3. reward 계산 (일치 여부 기준)
rewards = [1 if ans == majority_answer else 0 for ans in answers]
return rewards
3 Experiments
3.1 Experimental Setup
| 구성요소 | 설정 내용 | 이유 |
|---|---|---|
| Models | Qwen, LLaMA, Mistral, DeepSeek 등 다양한 scale의 LLM | pretrained + post-trained 모델 모두 사용 → TTRL이 전형적인 SFT 이후에도 작동 가능한지 검증 |
| Tasks | AIME 2024, AMC, MATH-500, GPQA | 정답이 명확하고 채점 가능한 task 위주 선택 |
| Sampling | 64개 생성, 32개 학습 사용 | label estimation 신뢰도 확보 + 연산 효율 고려 |
| Decoding | temp=0.6, top-p=0.95 | |
| RL Algorithm | GRPO, AdamW, Cosine schedule Learning rate:5 × 10⁻⁷ | 실험적으로 안정성과 sample-efficiency가 검증된 방식 |
| Max Length | 3072 (일반), 32768 (LRM) | CoT처럼 길고 reasoning-heavy한 답변도 처리 가능하도록 설계 |
| Episodes | AIME=80, AMC=30, MATH-500=10 | dataset 난이도와 크기에 맞춰 적절히 조정 |
Dataset 설명
AIME 2024 - American Invitational Mathematics Examination
AMC - American Mathematics Competitions
MATH-500 - Open-source 수학 문제집에서 500개 추출
GPQA - Graduate-level Physics Question Answering
3.2 Main Results
Table 1 : Performs well on most tasks
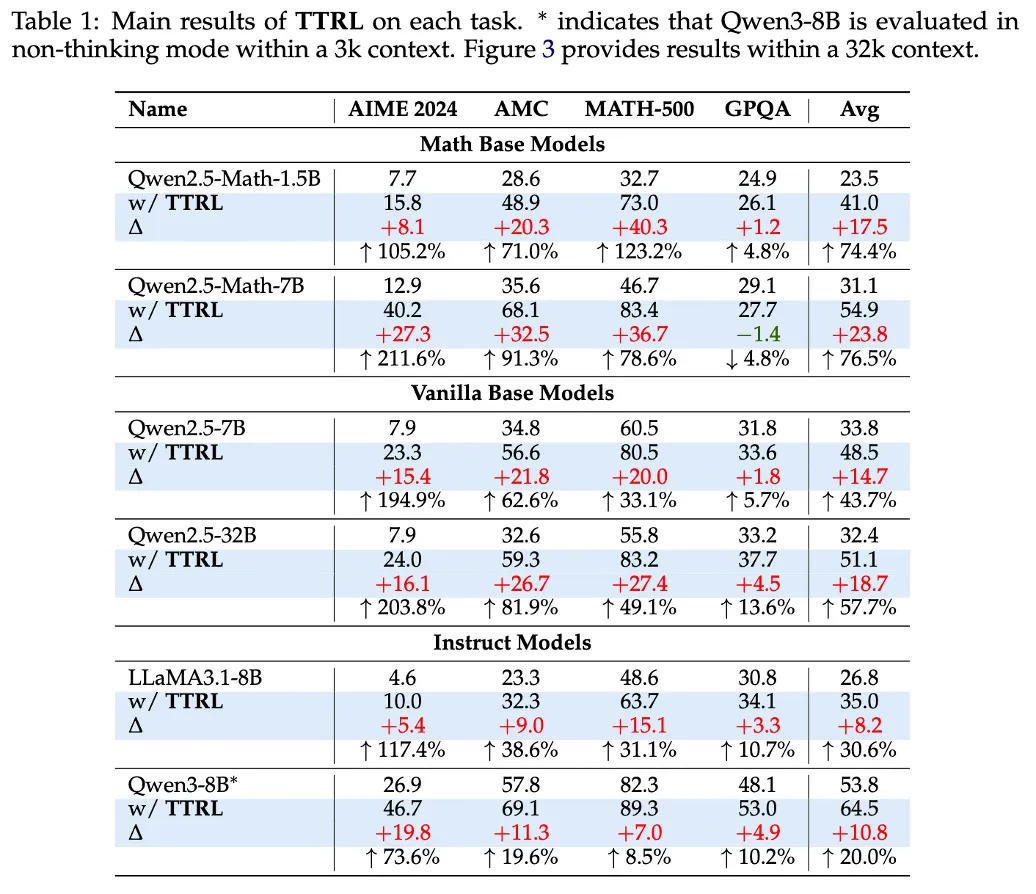
Qwen2.5-Math-1.5B 같은 1.5B 모델이 73.0까지 가기도 함.
→ 소형 모델은 RL이 어려웠다는 걸 깸
* 여기서는 Qwen3-8B가 non-thinking mode이고, thinking mode는 Figure 3
Table 2 : Performs well on most models
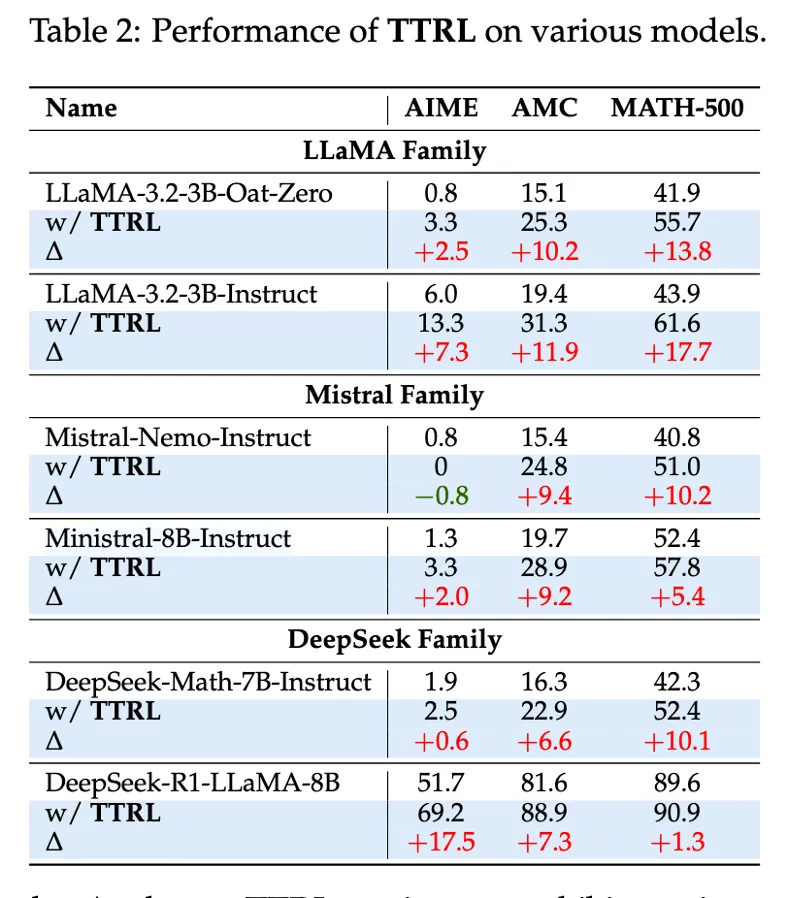
LLaMA-Instruct, DeepSeek-R1, Mistral 등 다양한 모델에서 테스트
Figure 3 : TTRL performs well on LRMs
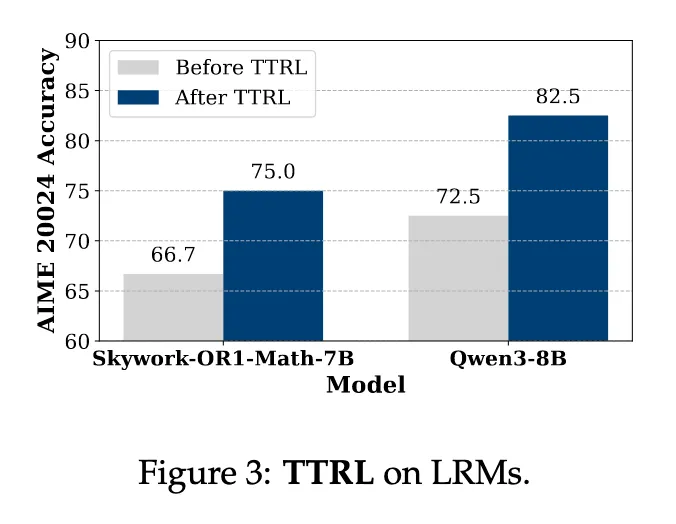
Large Reasoning Models에도 좋은 성능을 보임
이미 Reasoning쪽으로 타겟해서 학습한 모델도 향상됨
Figure 4 : TTRL generalizes well beyond the target task
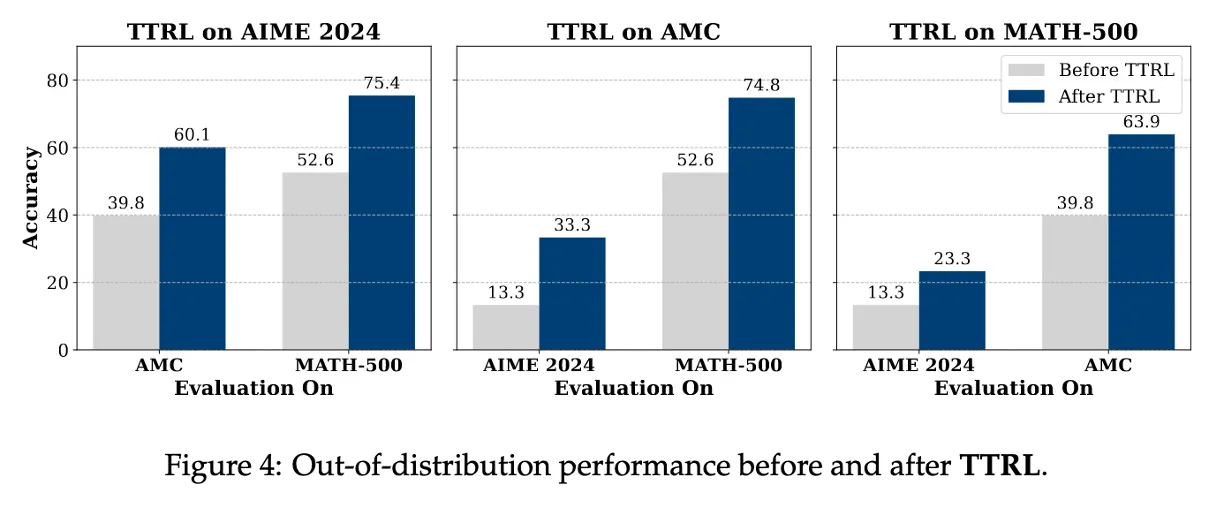
특정 벤치마크에서 학습 후 다른 task에서도 성능이 같이 올라감.
Figure 5 : TTRL is compatible with different RL algorithms
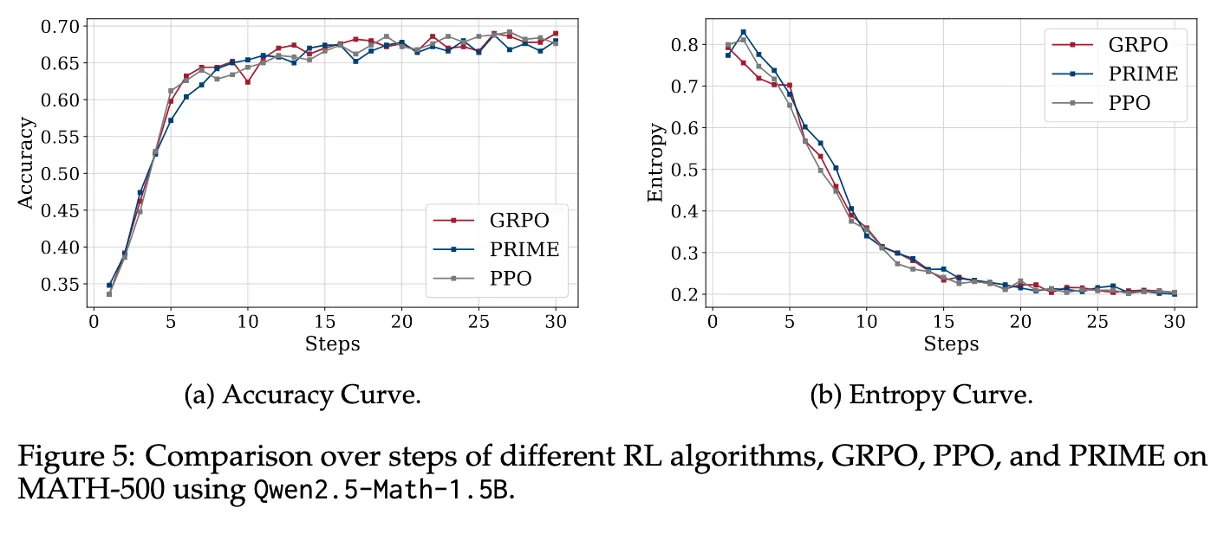
GRPO, PPO, PRIME을 비교
GRPO (rule-based), PPO (value-based), PRIME (process-level reward)
→ 다른 알고리즘으로도 호환이된다.
PPO : Proximal Policy Optimization
현재의 policy를 너무 많이 바꾸지 않으면서 조금씩 좋아지게
value function V(s) 을 사용해서 현재 상태가 얼마나 좋은지를 예측하고,
그 기준으로 얼마나 정책을 바꿀지를 계산
PRIME : Process Reinforcement through Implicit Rewards
https://arxiv.org/abs/2502.01456
각 토큰 단위로 계산된 log-prob ratio를 사용해 reward를 구성
근데, reward source는 여전히 majority voting 기반이었을 가능성이 큼
GRPO : Group Relative Policy Optimization
https://arxiv.org/abs/2402.03300
같은 질문에 대한 여러 응답의 상대적인 정답률을 비교하여 보상을 주는 방식
N개의 샘플, 다항 reward, 다양성 샘플링, online setting 등에 모두 적용 가능
DPO : Direct Preference Optimization (사용 안함)
두 응답 중 어느 쪽이 더 좋은지에 대한 인간의 "선호"를 직접 학습하는 방식
reward가 단순한 0/1 형태의 pairwise 비교로 제한
preference 들어가서 offline 구조임.
→ 이 논문에서 적용 못함.
Figure 6 : Achieves sustainable self-evolution through “online” and “RL”
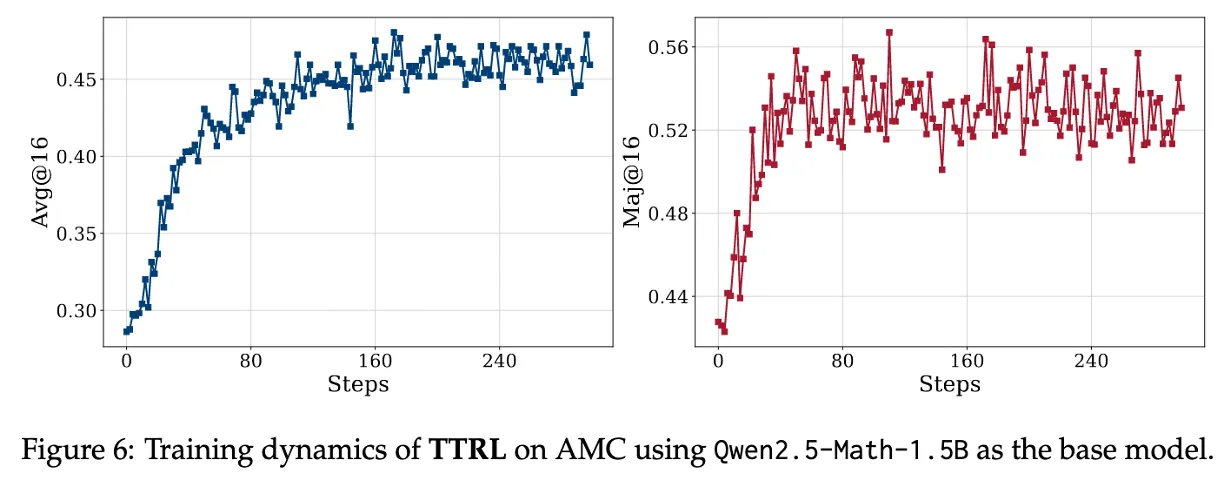
pass@1, avg@16, maj@16 이 뭐야?
pass@1
→ TTRL 모델이 현재 상태로 inference 할 때 단일 샘플이 정답일 확률
→ 실제 사용자 성능
avg@16
→ 예를 들어 정답이 10번 나왔으면 그 문제의 점수는 10/16
→ ground truth랑 비교해야하니까 사실상 나중에 성능 평가용임
maj@16
maj@64 accuracy
TTRL은 단순히 기존의 pseudo-label에 수렴하는 게 아니라, pseudo-label 자체도 계속 고도화되고 있음
이 논문에서는 RL을 쓸 때 maj@16 기준으로 reward를 계산(GRPO) 하고,
학습 이후 성능 평가에서는 avg@16, maj@16 둘 다 확인함.
4 Analysis and Discussions
4.1 Q1: How Well Can TTRL Perform?
기존 self-training 방식의 상한선들과 비교해서 어디까지 도달할 수 있는지 실험적으로 검증
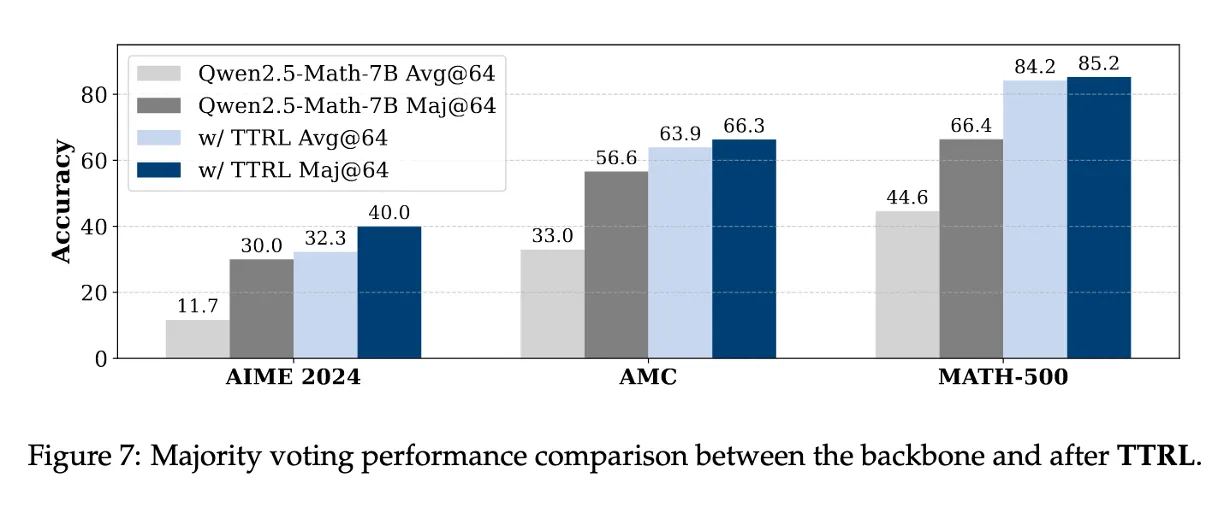
TTRL 전/후의 avg@64, maj@64 비교
→ 모든 benchmark에서 TTRL 적용 후 avg@64, maj@64 둘 다 성능이 증가
TTRL은 학습 신호로 maj@n을 사용했지만, 학습 이후 결과는 그 상한선을 초과
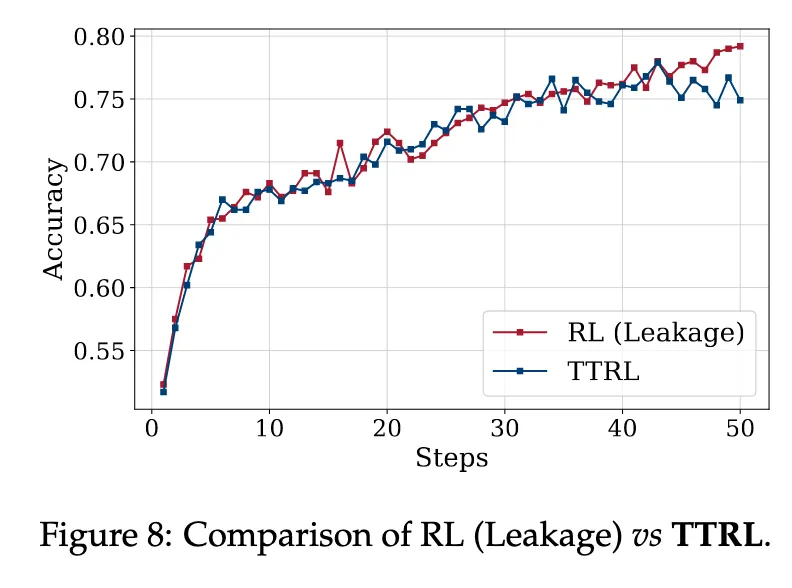
RL : ground-truth label이 있는 상태에서 RL을 직접 돌리는 경우
사실 RL은 Label이 없어서 Test-Time에 불가능 → 그 성능을 따라감
그런데 어떻게 TTRL이 중간 accuracy에서 leakage보다 높아질 수 있나?
Leakage RL은 단일 샘플에 대해 reward가 binary함
→ 이건 very sparse + very high variance reward
→ 따라서 초반에는 policy가 이 reward를 제대로 활용하기 어려움
반대로 TTRL은 soft한 avg 기반 reward를 사용함
하지만 시간이 지나면, 정답 기반 reward가 더 정확하므로 TTRL보다 더 높은 한계 성능에 수렴하게 됨
4.2 Q2: Why Does TTRL Work?
1. Label Estimation
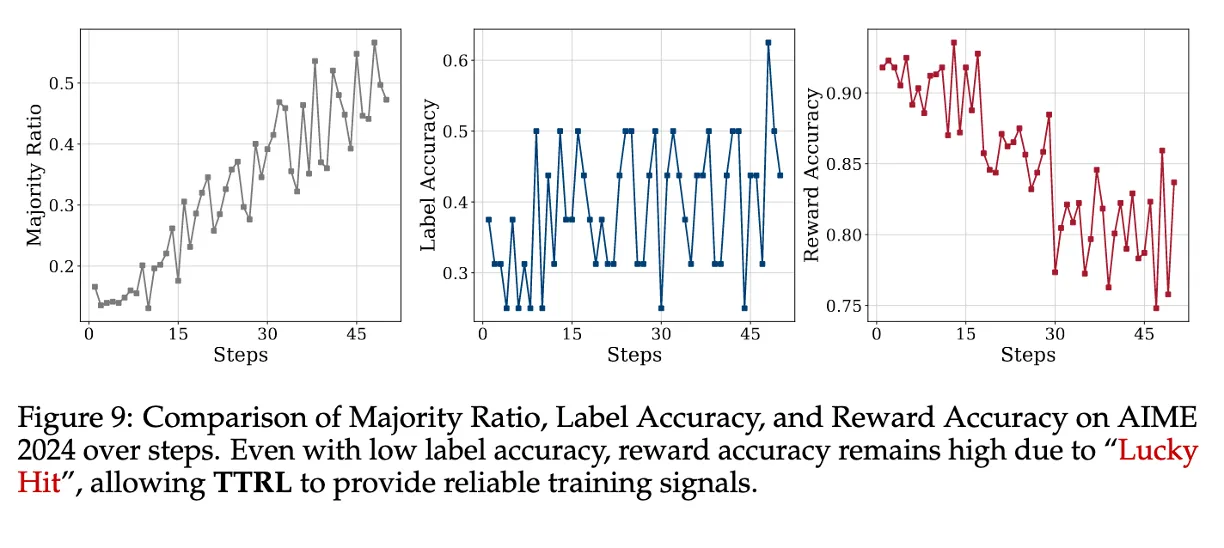
Label Accuracy와 Reward Accuracy는 다르다!!
라벨이 틀릴 수 있어도, reward는 우연히 맞기 때문에 보상 신호는 충분히 유효하고,
RL은 원래 그런 noise에 강하므로, label이 부정확해도 학습이 안정적으로 진행될 수 있다.
2. Reward Calculations
비교 기반이기 때문에 "운 좋게" 올바른 보상을 줄 수 있다
근데 이 label이 실제 정답이 아닐 수도 있음
그래도 ŷ가 틀린 label이랑도 다르면, 그건 "틀린 거다"라는 부정적 신호로는 여전히 맞음
→ label이 틀려도 reward는 우연히 맞는 경우가 많음

| 무엇을 기준으로 reward? | 예측값 | reward |
|---|---|---|
| True label (3) | 1 1 2 2 2 4 5 6 | 0 0 0 0 0 0 0 0 → 전부 오답 |
| Estimated label (2) | 1 1 2 2 2 4 5 6 | 0 0 1 1 1 0 0 0 → 3개 정답 처리 |
→ 8개 중 5개는 올바른 reward를 줌
rollout 기반 robustness
하나의 질문에 대해 여러 개 (M개)의 답변을 sampling하기 때문에:
모델이 못할수록 reward accuracy는 오히려 올라간다?
AIME 2024에서
모델이 다양한 오답을 내기 때문에 (e.g., 가장 많이 나온 답이 16.6%에 불과)
각각의 output이 다 다른 틀린 답이므로 → label과 일치하지 않음
그 자체로 negative reward가 제대로 전달됨 (비교 결과 다르니까)
3. Online Learning
온라인 RL 접근 방식을 기반으로 설계되니까 모델은 application하면서 기능을 향상시킬 수 있으며, 이는 투표를 통해 생성 된보다 정확한 레이블로 이어짐
→ supervision 신호의 품질이 향상되어 지속 가능한 자기 진화가 가능 (Figure 6 내용)
4.3 Q3: When Might TTRL Fail?
Figure 11 : Inappropriate RL Hyperparameters
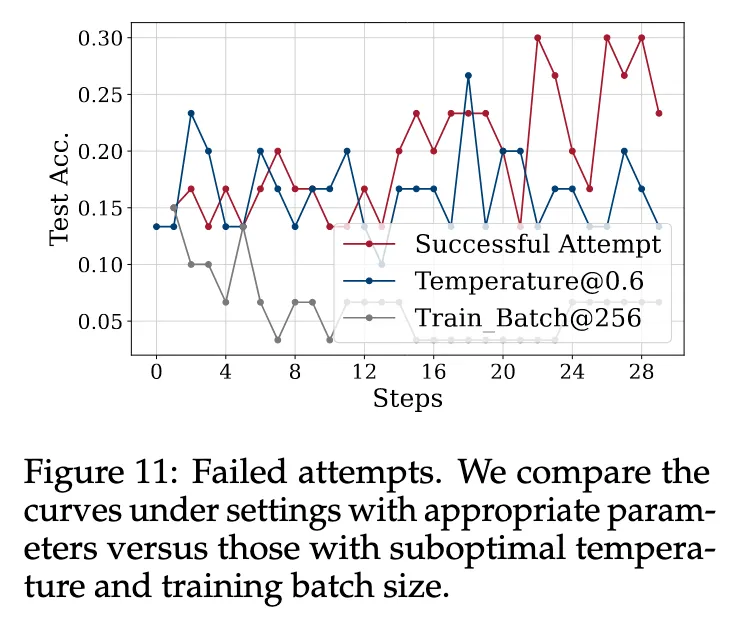
TTRL은 unsupervised + reward estimation이 noisy한 구조이기 때문에,
일반적인 RL보다 하이퍼파라미터에 훨씬 민감함.
(1) Temperature
T=1.0으로 높이면 더 많은 entropy (더 다양한 답변)(2) Episodes
→ TTRL은 문제의 난이도/분포/규모에 따라 하이퍼파라미터를 정밀 조정해야 함
Table 3: Lack of Prior Knowledge on Target Task
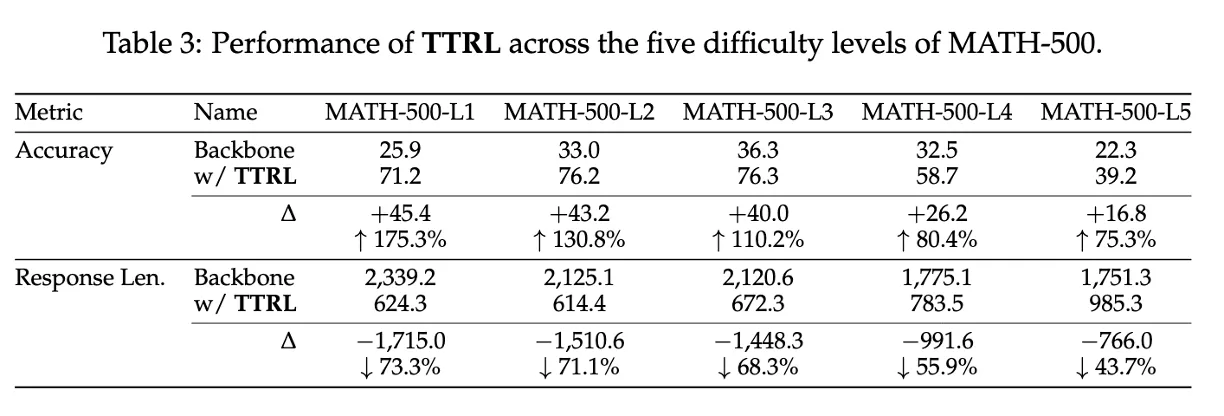
TTRL은 test set만 가지고 학습하기 때문에,
모델이 그 분야에 대한 사전 지식이 없으면 완전히 실패할 수 있음
→ 어려운 문제일수록 backbone의 사전 지식 부족으로 학습이 힘들다는 증거
7 Limitations and Future Works
Limitations
- TTRL은 초기 탐색 단계에 불과하며,
- 다음 두 요소가 학습 성능에 큰 영향을 미침에도 아직 정량적 분석이 부족함:
- 모델의 사전 지식 수준 (prior knowledge)
- 하이퍼파라미터 설정 (temperature, episode 수 등)
Future Works (논문에 나온 내용)
- 이론적 분석
- TTRL이 4.1에서 정의한 두 upper bound(maj@n / RL leakage)에 대해 얼마나 수렴 가능한지 이론적으로 분석
- convergence theory와 optimality 조건 규명
- 스트리밍 데이터 기반 온라인 학습
- 현재 TTRL은 static test set 기준
- 이를 실시간 도착하는 데이터 스트림에 적응하는 형태로 확장하려는 계획
→ 진정한 Test-Time Adaptation (TTA)으로의 확장
- 대규모 self-supervised RL
- TTRL을 대규모 데이터셋 + 대형 LLM에 적용
- 인간의 라벨링 없이도 강력한 자기지도 강화학습 시스템으로 발전시키려는 방향
- Agentic Task 및 과학적 추론
- TTRL을 단순 QA 또는 math benchmark가 아닌,
- 장기적 계획이 필요한 agentic task
- 여러 단계의 논리를 요하는 과학적 문제 해결에 확장
- open-ended한 domain으로도 TTRL 적용 가능성 타진
Limitations & Future Works (내 생각)
- Hyperparameter Sensitivity
RL training is highly sensitive to hyperparameters.
→Automatic hyperparameter tuning
- Too much resource
The experiments require 8 × A100 80GB GPUs
→ Parameter-efficient by LoRA
- Only for simple QA
Experiments are focused on math & multiple-choice
→ Extend to complex, multi-step reasoning tasks
Q&A
논문 Presentation 발표 중 제대로 답변 못한 Q&A
Q1) 이거 Test-Time에 RL 첫 논문 맞는가?
이론상 Test-Time + RL 구조의 첫 논문은 아니다.
GRPO 자체도 test-time에 쓸 수 있고, label 없이도 reward 만들 수 있지 않나?
https://arxiv.org/abs/2402.03300
GRPO를 소개한 DeepSeekMath
→ GRPO를 test-time에서 label 없이 쓰는 건 가능
TTRL에서 정의한 GRPO를 test-time에 실제로 쓰려면 필요한 요소들
→ 실제로 작동하게 만드는 환경 + 입력 + reward + 반복 학습 루프를 처음 설계
https://arxiv.org/abs/2505.18514
우리 연구실 지도교수님이신 공태식 교수님이 최근에 쓰신 이 논문도 “Test-Time RL”의 정의가 맞음
→ Test-Time RL의 최초라는 말은 틀림.
차이점은
BiTTA : 정답 클래스 자체는 필요하지 않지만, 실시간으로 사람의 Binary Feedback이 필요하다.
TTRL : 진짜로 label-free, oracle-free
정답이 있는 oracle의 binary feedback을 필요로 함.
TTRL은 어떠한 모델, 데이터셋에도 적용 가능하지만, (정답이 딱 떨어지기만 하면)
reward noise, model prior, dataset 난이도 등의 영향으로
hyperparameter (batch size, temperature, episode 수 등)에 매우 민감
→ 하이퍼파라미터 튜닝이 필요
Q2) Lucky hit여도 결국 틀린답으로 학습하는거 아닌가?
완전 잘못 이해하고 있었다. 내가 알고있던 정보는 BiTTA 처럼 Reward를 1과 -1로 줘야지 가능한 것이다.
https://arxiv.org/abs/2505.18514
예측이 틀렸으면 -1이라는 부정적인 보상을 명시적으로 줘서, 틀린 방향으로의 확률이 낮아지도록 gradient

예시 - 모델이 잘 모를때
[1, 1, 2, 2, 2, 4, 5, 6] → majority는 2 (2개)
→ 3/8이라서 적긴 하지만, 분명히 2가 정답이라는 것이 강화되는 건 맞다.
TTRL에서 모델이 잘 몰라서 majority voting을 통해 뽑은 pseudo label = 2
0 0 1 1 1 0 0 0
신호로 Reinforcement Learning
만약 실제로 true-label (3)을 줄 때
0 0 0 0 0 0 0 0
신호로 Reinforcement Learning
모델이 잘 모르는 것에 대해서 label이 없이 했지만,
실제 정답 label이 있을때와 Reward 신호가 62.5%나 일치한다! → hit ratio
실제 정답 라벨이 없기 때문에 다른 논문처럼 reward에서 penalty 신호인 -1을 주지 않고,
맞으면 1, 틀려도 0 으로 설정한 것으로 보인다.
Q3) 이 RL에서 action이 뭔가?
state : 주어진 문제(prompt) x
action : LLM의 답변 행위
→ LLM은 그에 대한 답변 y를 policy 로부터 생성 (sampling)