Test-Time Learning for Large Language Models
| ArXiv | https://arxiv.org/abs/2505.20633 |
|---|---|
| Authors | Jinwu Hu, Zhitian Zhang, Guohao Chen, Xutao Wen, Chao Shuai, Wei Luo, Bin Xiao, Yuanqing Li, Mingkui Tan |
| Affiliation | School of Software Engineering, South China University of Technology Pazhou Laboratory Zhejiang University South China Agricultural University Chongqing University of Posts and Telecommunications Key Laboratory of Big Data and Intelligent Robot, Ministry of Education |
Perplexity Minimization
기존 TTA (ex. Tent, EATA, COME)는 전부 entropy minimization 기반
→ 출력 분포의 불확실성을 낮추는 방향
하지만 이 논문은 LLM의 autoregressive 구조를 고려해
→ 출력 entropy가 아니라 입력 perplexity를 최소화하는 완전히 다른 objective를 제안
2. Related Work
기존 방법들의 특징과 LLM에서의 한계
Fine-tuning
: 라벨된 데이터를 기반으로 모델 파라미터를 업데이트
→ 라벨링 비용이 크고, 현실에서 계속해서 라벨된 데이터를 구하기 힘듦
RAG (Retrieval-Augmented Generation)
: 외부 지식 베이스에서 관련 정보를 찾아와 응답에 반영
→ 검색 품질에 의존 + 검색 비용 있음
TTT (Test-Time Training)
: 훈련 데이터나 knowledge base에서 유사한 데이터를 찾아서 모델을 미세 조정
→ 훈련 데이터 접근 필요 + 검색 과정이 느림
TTA (Test-Time Adaptation)
: 라벨 없는 테스트 데이터를 이용해 모델을 적응시킴
→ 대부분 entropy minimization (출력의 확률 분포를 단일하게 만드는 방식)을 사용
→ LLM은 autoregressive 구조인데, 이 구조를 무시하고 entropy만 최소화하면 효과가 떨어짐
기존 LLM TTA가 불가능한 이유
LayerNorm은 test-time에서 업데이트할 게 없음 → 기존 방식 적용 불가
그럼 LLM에서는 어떤 test-time 신호가 있는가?
→ 입력 perplexity를 이용해서
→ backprop 가능한 self-supervised objective를 설계함
Why Entropy Minimization Doesn’t Work Well for LLMs?
Entropy란?
entropy = uncertainty
[0.5, 0.5] → high entropy
[0.99, 0.01] → less entropy
Autoregressive한 LLM은?
Predict tokens one by one
Each prediction depends on previous tokens
Errors accumulate over time
문제점
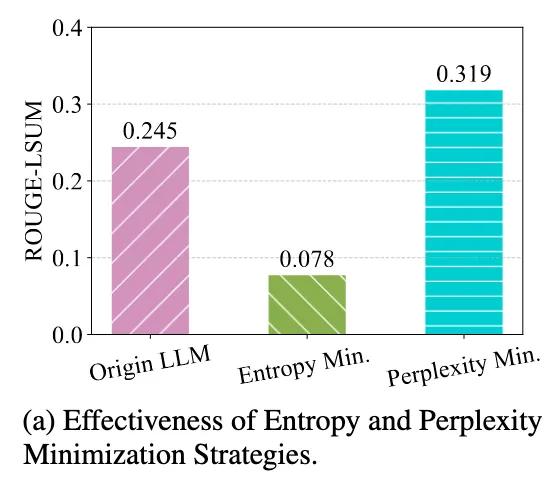
4.1 Perplexity Minimization for Test-Time Learning
Entropy 기반의 문제점 해결책
perplexity
: A metric that measures how confidently a language model predicts a given sequence
언어 모델이 주어진 시퀀스를 얼마나 “자신 있게” 예측했는가를 측정하는 지표
TTA에서의 문제점을 해결
entropy는 [p₁, p₂, ..., p_T] 각 토큰에 대해 개별적으로 확률 분포를 만들어서 토큰간의 관계보다는, 각 위치에서 단일 정답을 강하게 만들려고 함. → 토큰 간 dependency 무시
→ 시그마로 전체 시퀀스에 대한 joint probability의 log loss를 구하기 때문에 토큰 간 의존성을 완전히 반영함
→ 전체 문장을 얼마나 잘 예측했는가? 기준으로 loss 줌
→ 글로벌한 관점에서 모델을 업데이트
문제점
테스트 시엔 ground truth가 없음 → output perplexity를 못 씀
x = input / y = output
→ 발견
P(y | x)를 줄이는 대신 P(x)를 줄이는 것도 효과가 있다는 것
"The trend of LLM’s perplexity to the input P(x; Θ) and perplexity to the output P(y|x; Θ) is the same.”
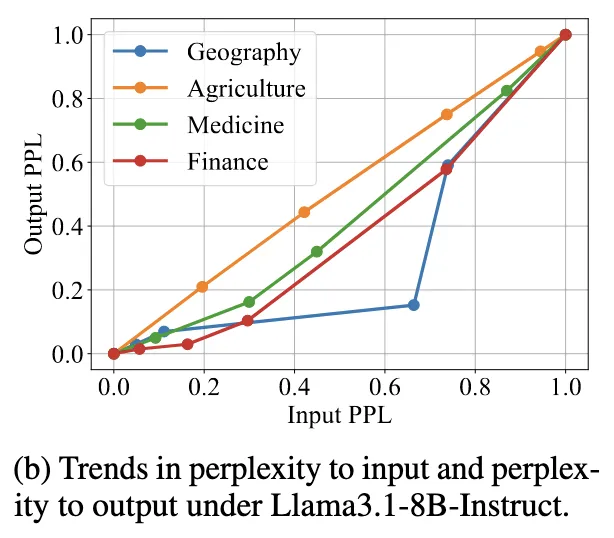
왼쪽 그래프를 보면,
input/output perplexity를 측정했을때
강한 상관관계를 보인다.
→ 입력 perplexity를 줄이면 출력도 같이 좋아짐
에서 y를 쓰지 않는 다음으로 변경
4.2 Sample Efficient Learning Strategy
TTL에서 모든 테스트 샘플을 다 사용해서 업데이트하면:
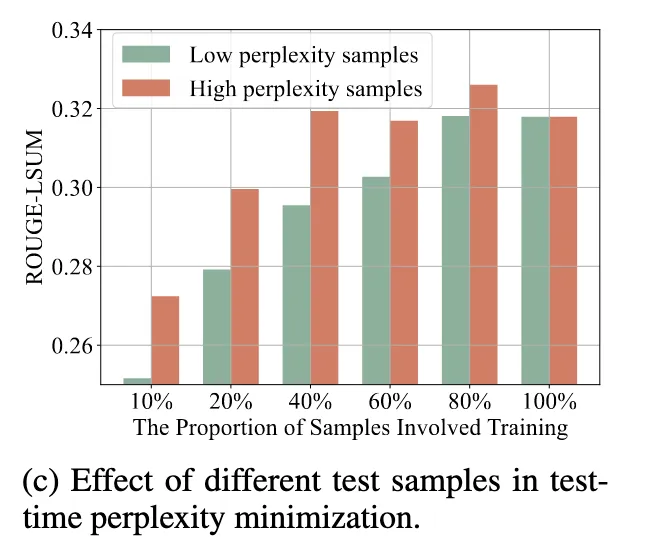
→ 발견
Low-perplexity input은 이미 잘 맞추는 것이라 정보 거의 없기 때문.
ROUGE(Recall-Oriented Understudy for Gisting Evaluation):자연어 생성 결과를 reference 문장과 비교해 얼마나 잘 일치하는지 평가하
ROUGE-L : Longest Common Subsequence (LCS) 기반으로 공통 부분문자열
Low-perplexity 샘플은 제외하고, High-perplexity 샘플은 비중을 크게 부여해서 학습에 반영
여기서 아라비아숫자 2 같이 생긴건, indicator function (지시 함수)를 의미한다.
즉, 조건을 만족하면 1, 만족하지 않으면 0이 되는 불연속 함수
효과
4.3 Modulating Parameters for Test-Time Learning
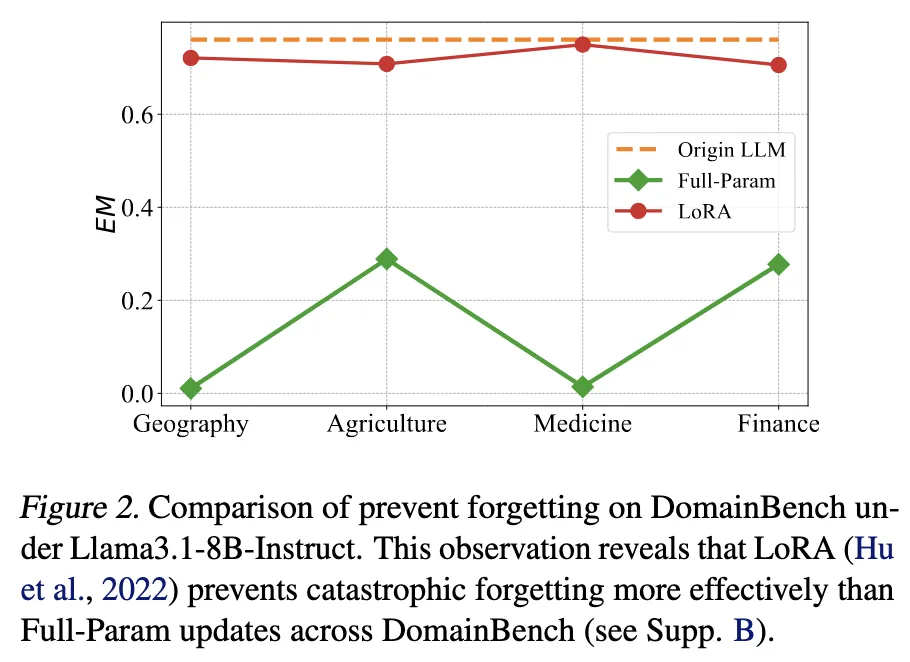
LoRA(Low-Rank Adaptation)는 일부 linear layer에 작은 랭크의 보조 행렬 A, B를 추가해서 업데이트함
→ LoRA로만 업데이트한 경우, full-param update보다 original 성능 유지력이 훨씬 좋음
도메인 적응 중에도 task 성능 유지 → forgetting 억제
LoRA를 사용하기 때문에 위와 같은 식이 됨
5.1. Experimental Settings
Benchmark: AdaptEval
| Bench | 목적 | 포함된 데이터셋 |
|---|---|---|
| DomainBench | 도메인 지식 적응 | Geography, Agriculture, Medicine, Finance |
| InstructionBench | 지시 따르기 | Alpaca-GPT4, Dolly, InstructionWild |
| ReasoningBench | 논리 추론 | GSM8K, MetaMath, Logiqa |
평가 지표 (Metrics)
각각의 task 특성에 맞는 대표 지표를 사용함
LLM 모델
Baselines
→ 모두 unlabeled test data만 사용하는 최신 TTA 기법
→ 공정한 비교를 위해 모두 offline 설정에 맞춰 재구현
구현 세팅
5.2 Comparison Experiments
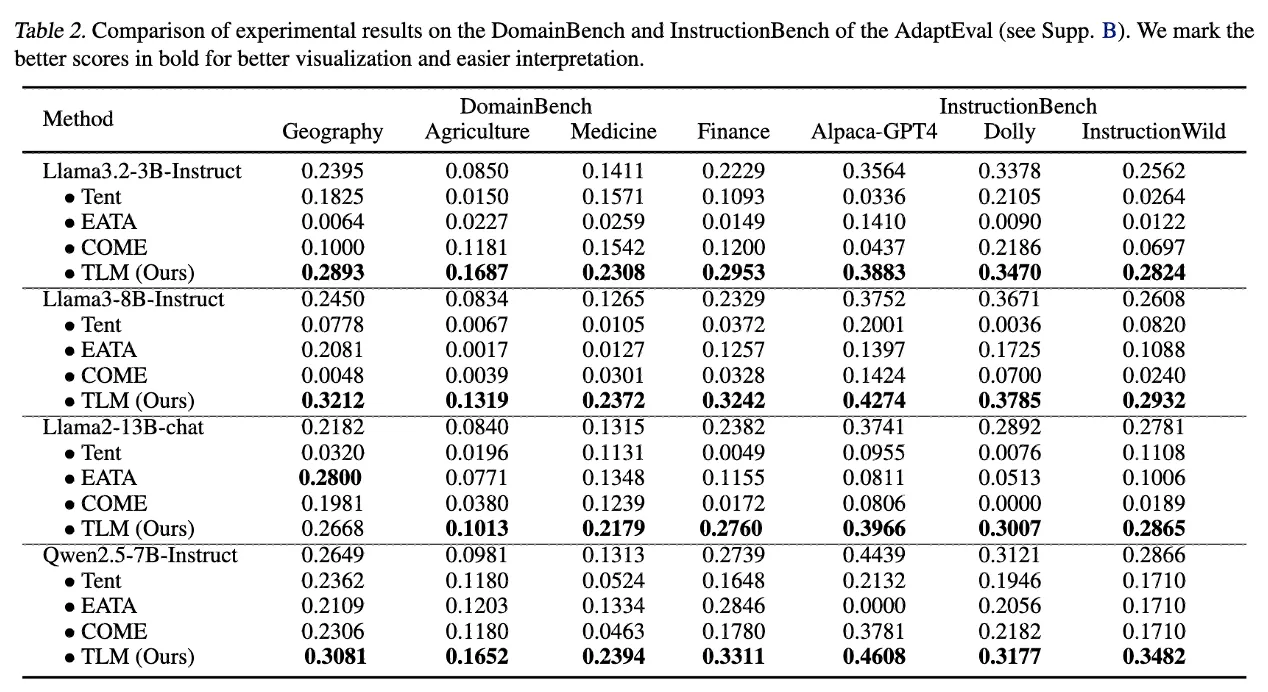
TLM은 모든 task category에서 baseline 대비 우수한 성능을 달성
→ 이런 과제들은 모델이 새로운 용어, 문장 패턴에만 적응하면 성능이 올라감
→ 그리고 TLM은 입력 perplexity 최소화 → 문장 표현에 대한 이해 강화
→ 즉, perplexity 기반 self-supervised 적응이 직접적으로 효과적임
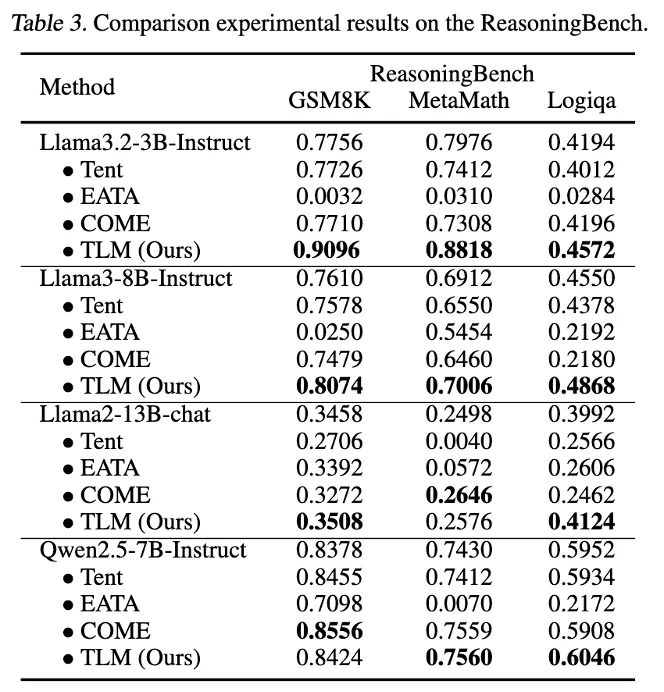
이 표만 값이 Exact Match (EM)임.
→ 정확히 답을 얼마나 맞췄는가
ReasoningBench도 좋아지긴 했지만, 논리 구조가 핵심이라 chain-of-thought reasoning이 중요함
→ test-time에 입력만 보고 모델을 개선하는 건 제한적인 효과만 있음
→ 특히 reasoning 능력은 이미 pretraining + fine-tuning 단계에서 깊게 학습되어야 함
5.3 Ablation Studies
| 버전 | 설명 |
|---|---|
| Original LLM | 아무런 TTL 적용 안 한 원본 |
| Ours (w/o SEL) | 샘플 선택 없이 input perplexity만 최소화 |
| Ours | full TLM = SEL + LoRA + perplexity minimization |
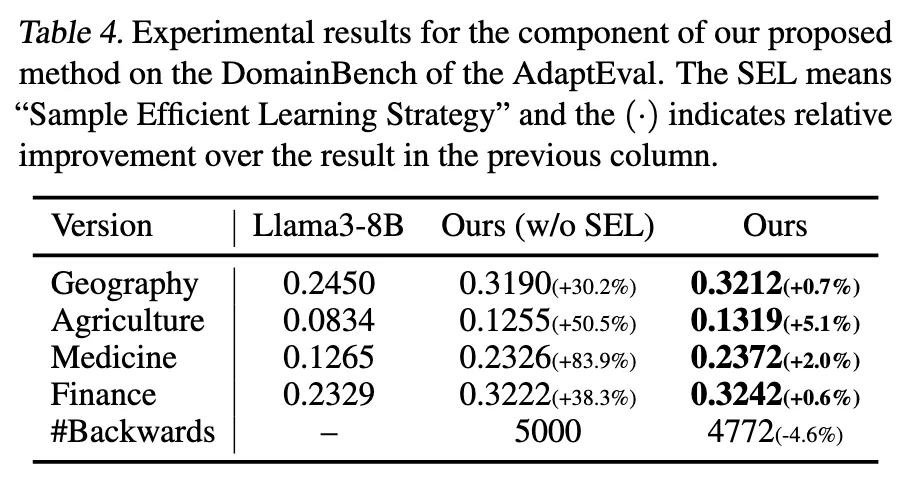
Input Perplexity Minimization
→ 성능 향상의 주된 원인
→ SEL 없이도 30~80% 향상
Sample Efficient Learning (SEL)
→ 추가 향상은 적지만,
→ 계산량 줄이면서 성능 유지
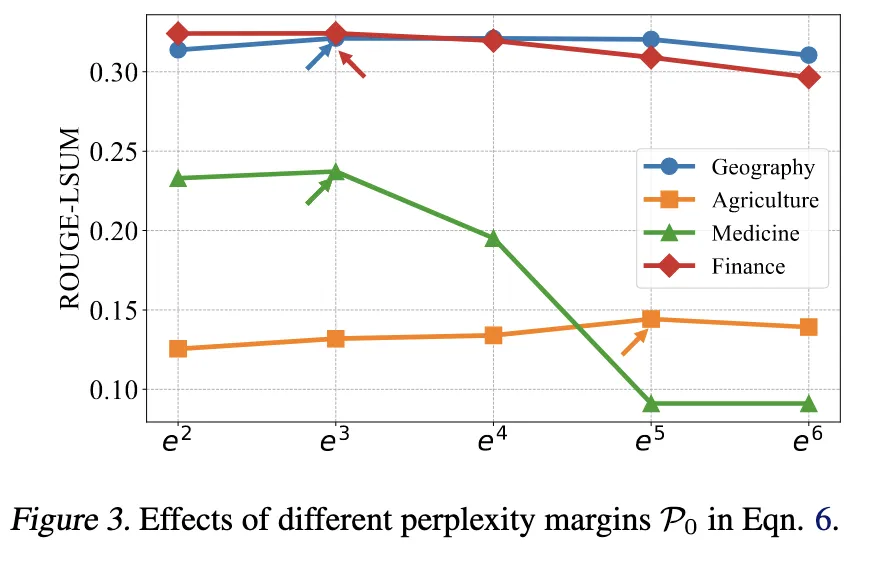
Threshold P0 (perplexity margin)
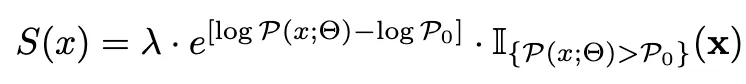
→다양한 P0∈{e2,e3,...,e6} 실험
→ P0=e3 일 때 가장 안정적이고 좋은 성능
5.4 More Discussions
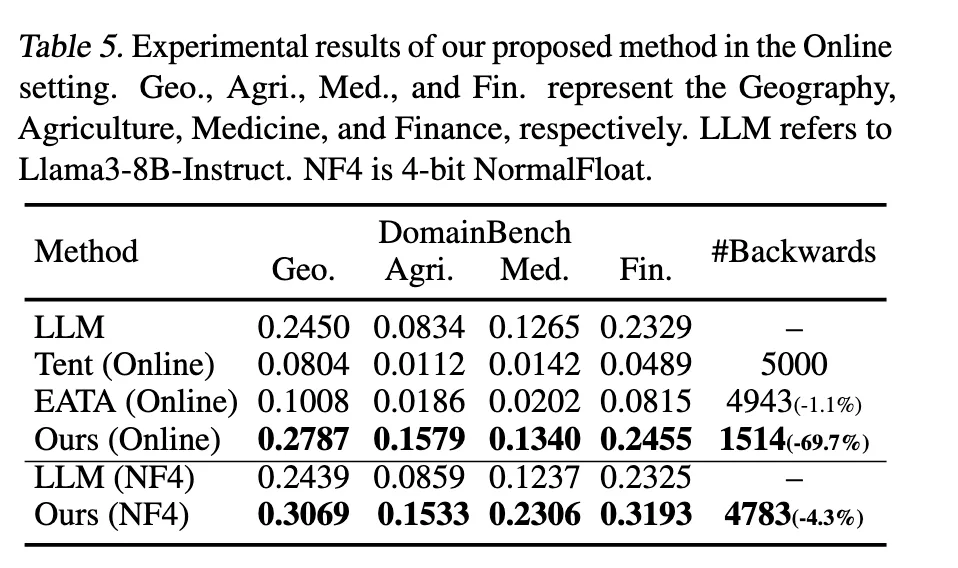
Online Test-Time Experiments
test-time에 샘플 하나씩 들어오는 상황에서도 TLM이 잘 작동하는가?
Experiments on Quantized LLM
TLM은 quantized 모델에서도 성능 향상 유지
→ 메모리 제한 환경에서도 실용적
Limitation
따로 언급은 없지만 굳이 뽑자면,
1. No Backprop-Free Variant (실제 inference 환경 제한)
TLM은 backprop이 필요함 → 대부분의 실제 LLM 배포 환경(API, closed-weight)에서는 적용 불가
Future Work: Backprop-free TTL, e.g. prompt-based or derivative-free adaptation
2. Limited Effect on Reasoning Tasks
GSM8K, MetaMath 등 reasoning benchmark에서 성능 향상폭이 작음
→ Perplexity minimization이 표현 적응에는 강하지만, 논리적 추론엔 약함
Future Work: TTL for logic and chain-of-thought reasoning
3. Domain-Specific Overfitting / Forgetting Risk
LoRA 사용해도, 장기적으로 특정 도메인에 반복 적응 시 원래 능력(logic, general knowledge) 저하 가능성 존재
Future Work: Continual TTL with forgetting mitigation
4. Hyperparameter Sensitivity (e.g., P₀ threshold)
샘플 선택 기준(P₀ = e³)이나 λ 값에 민감
도메인/모델에 따라 튜닝 필요 → 실용화에 방해될 수 있음
Future Work: Auto-tuning or adaptive sampling strategies
5. Session-Aware / Multi-Turn TTL 미지원
현재는 입력 단위로만 TTL 작동. 대화형 시스템처럼 context가 누적되는 환경에서는 적용되지 않음
Future Work: Session-level TTL for conversational agents
Q&A
Q. LLM에서 Test-Time 학습 최초인가?
다음과 같은 논문들은 있었음.
https://arxiv.org/abs/2410.08020
LLM을 테스트 시점에 prompt‑specific fine‑tuning 하는 방법을 제안했고,
실험을 통해 test‑time에도 LLM을 업데이트할 수 있다는 점을 보여줌
다만, 속도가 느리고 계산 비용이 크다는 단점
→ 가능은 했지만 실용에서 멀었음
Prompt tuning 빼면 TLM이 LLM에서 Test-Time 학습을 최초로 실용화한 논문
위 Table 5 를 보면 이미 Tent나 EATA도 한것처럼 보이지만, 오히려 기존 LLM을 파괴한 성능이 나옴.
Q. Output 내기 전에 학습하는 것인가?
P(y|x)을 기준으로 학습 못한다고 했는데, 왜? 어차피 output은 나오는거 아닌가?
왜 y를 안쓰는가?
모델이 생성한 ŷ는 정답이 아님 → ground truth 없음
P(ŷ | x)를 줄이면 잘못된 출력을 더 확신하게 만드는 결과가 될 수 있음
예시
순서
- 입력
x들어옴
- 모델이 현재 파라미터(θ + Δθ)로 출력
ŷ생성
-
x에 대한 perplexity 계산
-
P(x)가 기준보다 크면 → backprop으로 LoRA 파라미터 업데이트
- → 이 업데이트는 다음 입력부터 반영됨
정리
Although the true target y is unavailable at test time, we show that minimizing P(x) leads to update directions that are often aligned with those from minimizing P(y|x).
Test-time에 label y가 없어서 그 샘플의 성능을 직접 평가할 수 없음
→ 대신, 그 샘플을 기반으로 전체 파라미터를 업데이트해서 미래의 예측력을 높임
→ TLM은 online self-supervised continual learning에 가까움