💡
Key Differentiator “Outlier Absorption Using Singular Value Decomposition”
Song Han? Song Han is an associate professor at MIT EECS. He earned his PhD from Stanford, pioneering efficient AI computing techniques such as “Deep Compression” (pruning, quantization) and the “Efficient Inference Engine,” which first introduced weight sparsity to modern AI chips, making it one of the top-5 most cited papers in the 50-year history of ISCA (1953-2023). His innovations, including TinyML and hardware-aware neural architecture search (Once-for-All Network), have advanced AI model deployment on resource-constrained devices.
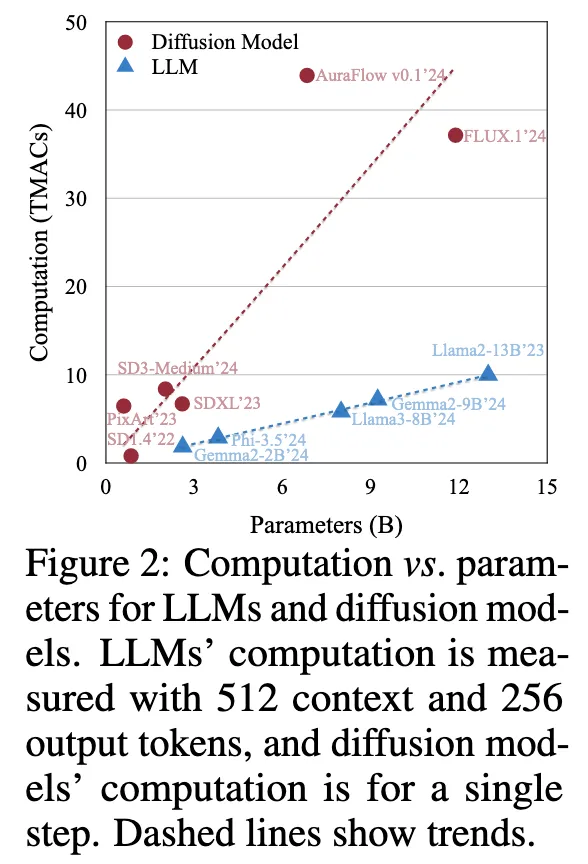
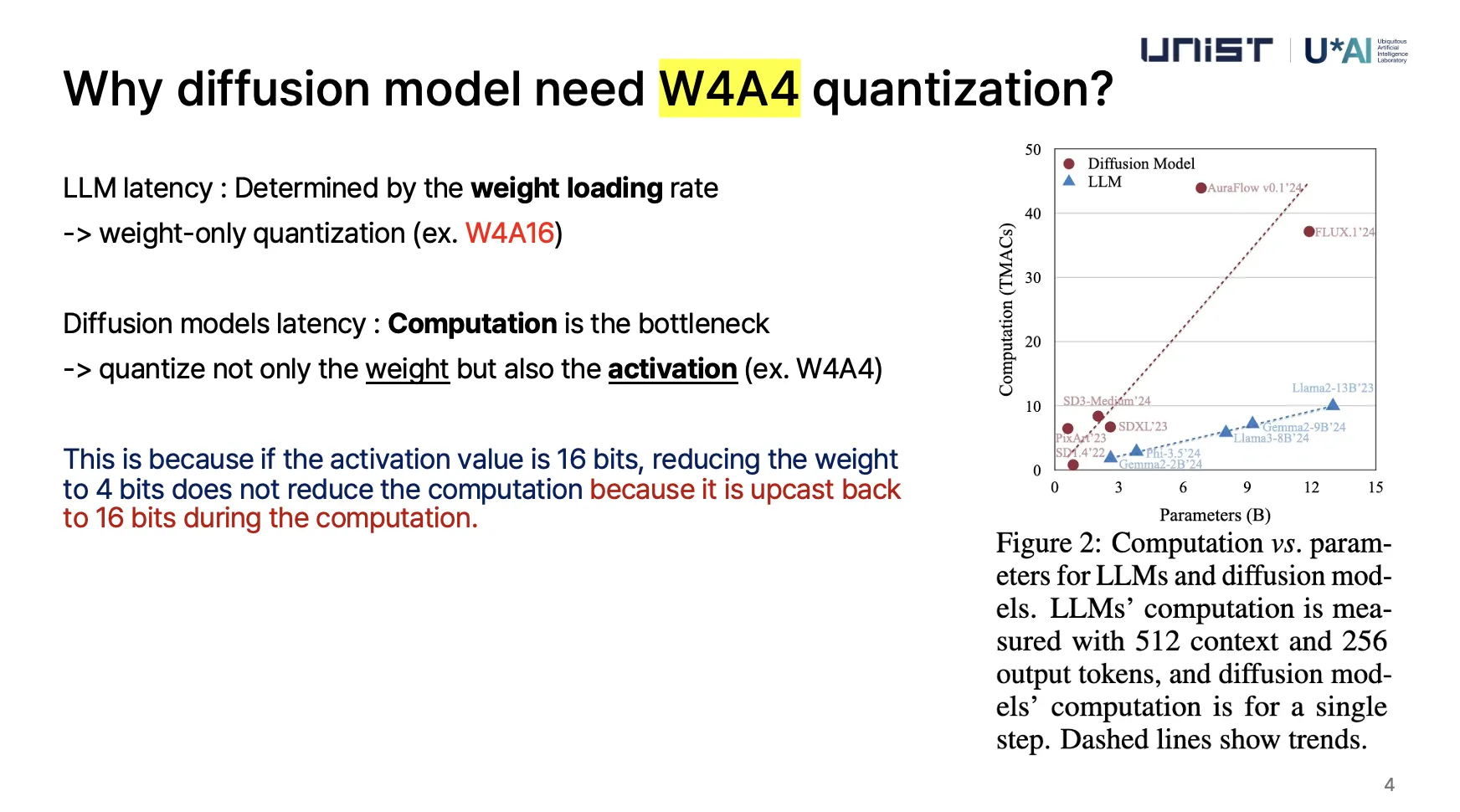
1. Introduction LLM과 비교했을 때, 모델 사이즈에 따라 계산 비용이 빠르게 증가한다.
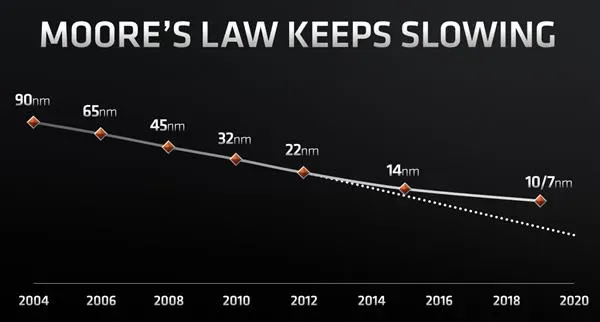
Moore’s law가 slow down 함으로서, 저렴한 추론(low-precision inference) 으로 전환하는중
→ 4bit floating point (FP4)가 대세임
LLM
latency는 주로 가중치(weight) 로딩 속도에 의해 결정
"가중치만 양자화(weight-only quantization)" 해도 속도를 개선
Diffusion 모델
레이턴시는 가중치를 불러오는 속도가 아니라, 연산량 자체가 병목
왜냐하면 가중치만 4비트로 줄여도 활성화값이 16비트이면, 연산 과정에서 16비트로 다시 변환(upcast)되므로 연산량이 줄어들지 않음.
결국 연산량을 줄이려면 가중치(weight)뿐만 아니라 활성화값(activation) 도 함께 4비트로 양자화해야 함.
📢
Input Channel → 원래 Activation에서 나온 입력 채널 Channel → Weight의 각 채널
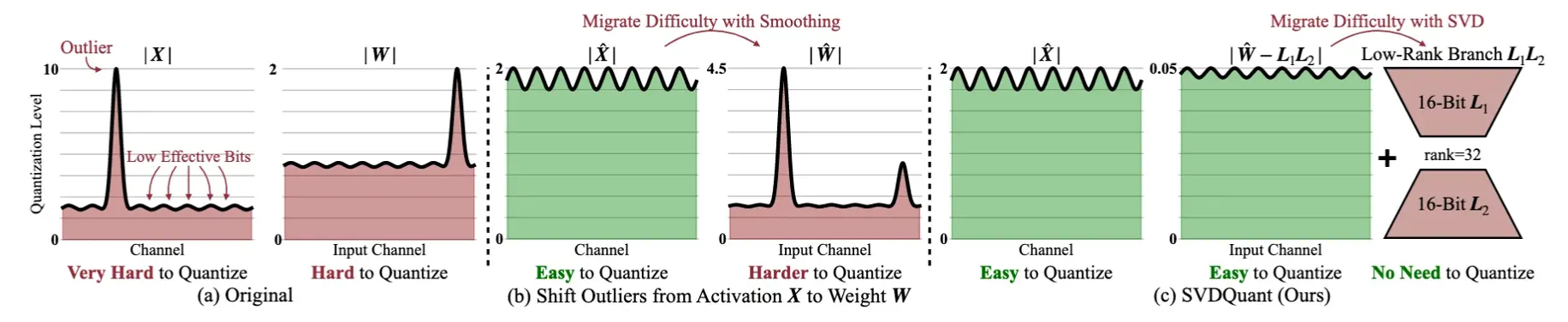
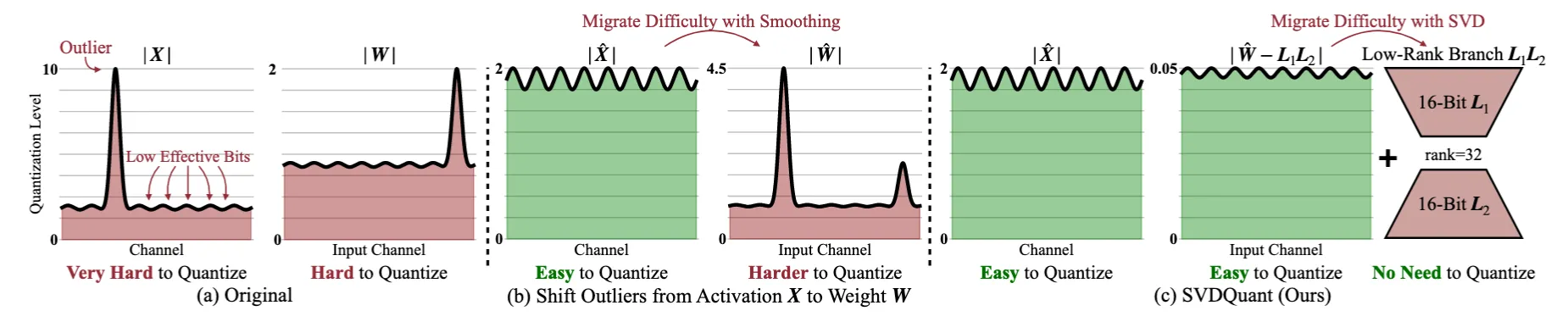
1. 기존 4비트 양자화(4-bit Quantization)의 문제점 가중치(Weight)와 활성화값(Activation) 모두 4비트로 줄이면 품질이 크게 저하될 가능성이 높음. 특히 기존 방법(예: Smoothing)은 가중치와 활성화값 사이에서 Outlier를 이동시키는 방식을 사용했지만,Diffusion 모델에서는 Outlier가 양쪽(W, X) 모두에서 심각하게 발생하므로 효과적이지 않음. 기존 방식은 활성화값(X)에서 Outlier를 제거하려고 하면 가중치(W)로 이동하고, 반대로 하면 X에 Outlier가 남는 문제 발생. 2. SVDQuant의 핵심 아이디어 Outlier를 단순히 이동하는 것이 아니라, " 흡수 "하는 방법을 사용함. 저비용의 "Low-Rank Branch"를 추가하여 Outlier를 가중치(W)에서 흡수함. 이를 위해 SVD(Singular Value Decomposition, 특이값 분해) 기법을 활용하여 가중치를 두 개의 성분으로 분해함. 3. SVDQuant의 단계별 동작 방식 1. Outlier 이동 (Smoothing)
먼저 Outlier를 활성화값(X)에서 가중치(W)로 이동함. 이를 통해 활성화값(X)이 더 균일해져서 4비트 양자화가 더 쉬워짐. 2. SVD(특이값 분해)를 적용하여 가중치(W)를 두 개의 성분으로 분해
W → L1L2(저순위 성분) + 잔여 성분(W - L1L2)로 분리 L1L2(저순위 성분)은 16비트로 유지하고, W - L1L2(잔여 성분)만 4비트로 양자화 즉, 저순위 성분(Low-Rank Component)이 Outlier를 흡수하면서 4비트 양자화가 더 쉬워짐. 3. 저순위 성분을 따로 계산하면 메모리 액세스 오버헤드가 증가하는 문제 발생
즉, L1L2를 별도로 처리하면 연산 속도가 느려지는 문제가 생김. 기본적으로 4비트 연산의 속도를 높이려고 했는데, 저순위 연산이 추가되면 오히려 느려질 수 있음. 4. 이를 해결하기 위해 전용 추론 엔진(Nunchaku) 설계
Nunchaku 엔진은 4비트 양자화 연산과 저순위 연산을 함께 최적화하여 오버헤드를 줄임. 즉, L1L2(저순위 연산)와 4비트 연산을 함께 처리하는 커널(fusion kernel)로 변환하여 성능을 최적화. 이를 통해 추가적인 연산량이 생기더라도 실제로는 4비트 연산의 속도를 향상할 수 있도록 설계됨.
기존 방식(SmoothQuant, AWQ)과 SVDQuant의 차이 방법 방식 Outlier 처리 방식 적용 대상 문제점 SmoothQuant (2023) W4A4 Input Channel(Activation) → Channel(Weight) LLM(대형 언어 모델) Outlier가 가중치에 누적됨 AWQ (2024) W4A4 가중치 중 중요한 부분을 보존하여 양자화 LLM Diffusion 모델에서는 한계 가능성 SVDQuant (2024) W4A4 저순위(Low-Rank) 성분으로 Outlier 흡수 Diffusion 모델 최적화 추가 연산을 해결해야 함
1. SmoothQuant (2023) – Activation에서 Weight로 이상치 이동 SmoothQuant의 핵심 아이디어는 활성화값(Activation)에서 발생하는 이상치를 가중치(Weight)로 이동 시키는 거야Li 등 - 2024 - SVDQuan….
기존 문제 Transformer 기반 모델에서 Self-Attention 연산이 많아서 활성화값(Activation)의 범위가 넓어지고 이상치가 발생 하는 경우가 많아. 이를 8-bit이나 4-bit로 양자화하면, 작은 값들은 모두 0이 되고, 정보 손실이 심해짐. 해결 방법 활성화값(Activation)의 채널별 스케일링을 적용하여, 이상치를 가중치(Weight) 쪽으로 이동 시킴. 즉, 원래 Activation 값이 크면, 해당 채널을 스케일링해서 줄이고, 대신 그 값을 Weight에서 보상해주는 방식. 이렇게 하면, Activation 값이 양자화할 때 손실 없이 더 균등하게 분포할 수 있음 . 한계 Weight 쪽으로 이상치를 몰아넣으면, Weight의 값이 커지고, Weight 양자화 시 오류가 커질 가능성 이 있음. 따라서 Weight를 4-bit로 양자화할 경우 정보 손실이 발생할 수 있음 . 2. AWQ (Activation-aware Weight Quantization, 2024) – Weight에서 Activation으로 이상치 이동 AWQ는 Weight의 이상치를 줄이기 위해 Activation으로 분산시키는 방식
기존 문제 SmoothQuant 방식처럼 이상치를 Weight 쪽으로 이동시키면, Weight의 크기가 커져서 Weight를 4-bit로 양자화할 때 정보 손실이 발생 할 가능성이 높아짐. 특히, Weight에 이상치가 많으면, 스케일링을 적용해도 양자화 오류가 커지고 성능이 떨어지는 문제 가 발생. 해결 방법 대신 Weight에서 Activation으로 일부 이상치를 이동시켜서, Weight가 양자화될 때 정보 손실을 최소화 함. 즉, 중요한 Weight 값을 따로 보호하고, 불필요한 큰 값을 Activation 쪽으로 이동시켜서 Weight를 더 균등한 분포로 만들도록 설계. 한계 Activation의 분포가 다시 넓어질 가능성이 있음 → Activation을 다시 4-bit로 양자화할 경우 문제가 발생할 수도 있음 . 3. SVDQuant (2024) – Outlier를 Low-Rank Component로 이동 SVDQuant는 SmoothQuant와 AWQ의 문제점을 모두 해결하려고, 이상치를 이동시키는 것뿐만 아니라 Low-Rank Component로 흡수 하는 방식이야Li 등 - 2024 - SVDQuan….
핵심 아이디어 SmoothQuant처럼 Activation의 이상치를 Weight로 이동 하면서도, AWQ처럼 Weight에서 다시 Activation으로 이동하는 대신, Low-Rank Component로 분리하여 저장 . 즉, 이상치를 양자화하지 않고, 16-bit Low-Rank Component로 유지 하여 정보 손실을 최소화. 장점 SmoothQuant나 AWQ처럼 한쪽으로 이상치를 몰아넣지 않고, Low-Rank Branch가 이상치를 흡수해서 손실을 막음 . Weight와 Activation 모두 균등한 분포를 가지게 되어, 양자화 오류가 줄어듦 . 실제 실험에서도 SmoothQuant, AWQ보다 4-bit 양자화에서 성능이 뛰어남 . 결론 SmoothQuant → Activation의 이상치를 Weight로 이동 (Weight의 정보 손실 가능성 있음) AWQ → Weight의 이상치를 Activation으로 이동 (Activation의 정보 손실 가능성 있음) SVDQuant → Weight와 Activation에서 Low-Rank Component로 이동 (이상치 자체를 제거하여 정보 손실을 최소화) 즉, SmoothQuant과 AWQ는 둘 중 하나만 Outlier를 발생하지 않도록 하려고 했던 접근법 , 반면 SVDQuant는 Outlier 자체를 Low-Rank로 빼버리는 방식이라 정보 손실이 가장 적음 .
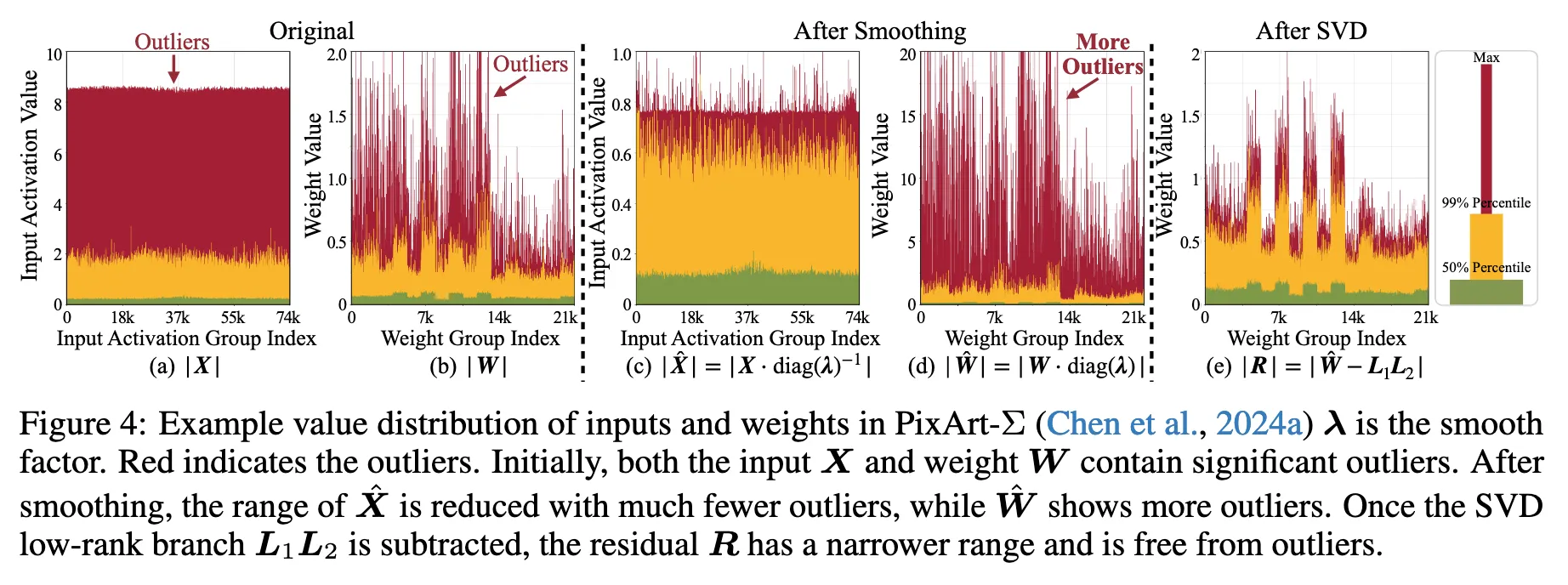
3 QUANTIZATION PRELIMINARY 양자화(Quantization)의 기본 개념 딥러닝에서 양자화는 연산 속도를 높이고 메모리 사용량을 줄이는 데 사용되는 방법 . 텐서 X를 양자화하는 과정: Q X = r o u n d ( X s X ) , s X = max ( ∣ X ∣ ) q m a x . Q_X = \mathrm{round}\left( \frac{\mathbf{X}}{s_X} \right), \quad s_X = \frac{\max(|\mathbf{X}|)}{q_\mathrm{max}}. Q X = round ( s X X ) , s X = q max max ( ∣ X ∣ ) . 여기서 QX는 양자화된(low-bit) 값 . sX는 스케일링 팩터(Scaling Factor) . qmax는 최대 양자화 값 (비트 수에 따라 달라짐). 4비트 부동소수점 양자화(4-bit FP)에서는 qmax=6임. 양자화된 행렬 연산 선형 계층(Linear Layer)에서 입력 X와 가중치 W가 있을 때, 연산을 양자화된 값으로 근사: X W ≈ Q ( X ) Q ( W ) = s X s W ⋅ Q X Q W . \mathbf{XW} \approx Q(\mathbf{X}) Q(\mathbf{W}) = s_X s_W \cdot Q_X Q_W. XW ≈ Q ( X ) Q ( W ) = s X s W ⋅ Q X Q W . 즉, 양자화된 텐서끼리 연산한 후, 스케일링 팩터 sXsW를 곱하여 다시 원래 값에 가깝게 복원함. GPU에서 같은 비트폭(bit width)을 사용해야 하는 이유 최신 GPU에서는 입력(QX)과 가중치(QW)의 비트 수가 동일해야 연산 속도가 향상됨. 만약 QX와 QW의 비트 수가 다르면, 더 높은 비트 값으로 변환(upcast)되면서 속도 이점이 사라짐. 예: 가중치(W)를 4비트로 양자화(W4)했지만, 활성화값(X)이 16비트(A16)라면? 연산 시 W4가 A16으로 업캐스트(Upcast)되어 실제 속도 향상이 없음. W4A4(가중치 4비트, 활성화값 4비트) 조합이 최적화된 방식. </br> W4A4 양자화에서의 문제점: Outlier(이상치) Diffusion 모델에서는 가중치(W)와 활성화값(X) 양쪽에서 Outlier(극단적인 값)가 많이 발생 함. Outlier가 많으면 양자화 후 품질이 크게 저하됨. 기존 해결 방법: Quantization-Aware Training (QAT) 양자화를 고려하여 모델을 훈련하는 방식. 하지만, 100억 개 이상의 매개변수(예: FLUX.1 모델)를 조정하려면 계산 비용이 매우 큼. Rotation 기법 (Ashkboos et al., 2024; Liu et al., 2024c) 가중치와 활성화값을 회전(rotation)하여 Outlier를 줄이는 방법. 하지만, Diffusion 모델의 "Adaptive Normalization Layer"에서는 적용이 어려움. 이유: Adaptive Normalization은 실행 시간(runtime) 중에 새로운 가중치를 생성 . 따라서, 사전 계산된 회전 행렬을 적용할 수 없음. 실행 시간에 회전을 적용하면 연산량이 증가하여 속도가 느려짐.
📢
이상치(Outlier)가 있으면 어떻게 성능이 저하될까?
1. 스케일링 팩터 문제 양자화는 데이터의 전체 범위(min-max)를 고려해서 값을 조정해야 하는데, 이상치가 있으면 스케일링 팩터가 비정상적으로 커짐 . 대부분의 값은 작은 범위에 몰려 있는데, 한두 개의 큰 값(이상치) 때문에 스케일이 커지면 작은 값들이 모두 0 또는 동일한 값으로 매핑되는 문제 가 생겨. 예제: 원래 가중치 값: [-0.1, -0.05, 0.0, 0.05, 0.1, 5.0] (이상치: 5.0) 이상치가 없을 때: s_X = 0.1, 범위를 [-8, 7]로 매핑 가능 이상치(5.0)가 포함될 때: s_X = 5.0, 작은 값들은 모두 0이 되어 정보 손실 발생 2. 정보 손실 (Precision Loss) 이상치를 고려해 전체 값을 조정하면, 나머지 대부분의 값이 매우 작은 차이를 가지는데도 동일한 양자화된 값으로 표현 될 가능성이 높아. 즉, 모델이 작은 변화(gradient 등)를 반영하지 못하고 표현력이 급격히 떨어짐 . 3. 활성화(Activation) 이상치로 인해 연산량 증가 이상치가 있으면 양자화된 값을 다시 부동소수점으로 변환할 때 FP32(32-bit)로 변환하는 경우가 많아 , 결국 연산 최적화가 깨짐. 특히 Transformer 기반 모델에서는 Self-Attention 연산이 크기 때문에 활성화값(Activation)의 이상치는 메모리 사용량과 연산량 증가로 이어질 수 있음 . 4 Method
4.1 PROBLEM FORMULATION 양자화의 오류를 다음과 같이 정의됨.
E ( X , W ) = ∥ X W − Q ( X ) Q ( W ) ∥ F E(\mathbf{X}, \mathbf{W}) = \left\| \mathbf{XW} - Q(\mathbf{X}) Q(\mathbf{W}) \right\|_F E ( X , W ) = ∥ XW − Q ( X ) Q ( W ) ∥ F 원래 행렬 곱셈 XW와 양자화된 값으로 연산한 Q(X)Q(W)의 차이를 측정하는 값
좀 더 세분화
E ( X , W ) ≤ ∥ X ∥ F ∥ W − Q ( W ) ∥ F + ∥ X − Q ( X ) ∥ F ( ∥ W ∥ F + ∥ W − Q ( W ) ∥ F ) . E(\mathbf{X}, \mathbf{W}) \leq \left\| \mathbf{X} \right\|_F \left\| \mathbf{W} - Q(\mathbf{W}) \right\|_F+ \left\| \mathbf{X} - Q(\mathbf{X}) \right\|_F \left( \left\| \mathbf{W} \right\|_F + \left\| \mathbf{W} - Q(\mathbf{W}) \right\|_F \right). E ( X , W ) ≤ ∥ X ∥ F ∥ W − Q ( W ) ∥ F + ∥ X − Q ( X ) ∥ F ( ∥ W ∥ F + ∥ W − Q ( W ) ∥ F ) . 이 식은 양자화 오류를 결정하는 네 가지 요소를 보여줌:
가중치의 크기: ∥ W ∥ F \|\mathbf{W}\|_F ∥ W ∥ F 입력의 크기: ∥ X ∥ F \|\mathbf{X}\|_F ∥ X ∥ F 가중치의 양자화 오류: ∥ W − Q ( W ) ∥ F \|\mathbf{W} - Q(\mathbf{W})\|_F ∥ W − Q ( W ) ∥ F 입력의 양자화 오류: ∥ X − Q ( X ) ∥ F \|\mathbf{X} - Q(\mathbf{X})\|_F ∥ X − Q ( X ) ∥ F 즉, 전체적인 양자화 오류를 최소화하려면 이 네 가지 요소를 조절하는 것이 핵심임.
4.2 SVDQUANT: ABSORBING OUTLIERS VIA LOW-RANK BRANCH Migrate outliers from activation to weight After Smoothing 부분이 기존 기법인데, 단점이 있음
✅ Activation(X)의 이상치를 없애는 것은 성공했지만 , ❌ 대신 Weight(W)의 이상치가 증가하는 문제가 발생 . 결과적으로, 전체적인 양자화 오류를 줄이려는 목적이 제대로 달성되지 않음 .
Absorb magnified weight outliers with a low-rank branch. Weight를 바로 4-bit로 양자화하지 않고, Low-Rank Component를 따로 분리해서 이상치를 흡수 하는 전략
W ^ = L 1 L 2 + R , where L 1 ∈ R m × r and L 2 ∈ R r × n \hat{\mathbf{W}} = \mathbf{L}_1 \mathbf{L}_2 + \mathbf{R}, \quad \text{where } \mathbf{L}_1 \in \mathbb{R}^{m \times r} \text{ and } \mathbf{L}_2 \in \mathbb{R}^{r \times n} W ^ = L 1 L 2 + R , where L 1 ∈ R m × r and L 2 ∈ R r × n L 1 = U Σ r \mathbf{L}_1 = \mathbf{U} \boldsymbol{\Sigma}_r L 1 = U Σ r L 2 = V r T \mathbf{L}_2 = \mathbf{V}_r^T L 2 = V r T R \mathbf{R} R
SVD(Singular Value Decomposition, 특이값 분해) 원래 행렬 크기가 m×n이면, 직접 곱하면 연산량이 O(mn) . 하지만 SVD로 Rank r만 유지하면 연산량이 O(mr+rn)로 줄어듦 . U \mathbf{U} U ( m × m ) (m \times m) ( m × m ) Σ \boldsymbol{\Sigma} Σ m × n m \times n m × n V T \mathbf{V}^T V T ( n × n ) (n \times n) ( n × n )
포인트는 대각 원소(특이값, Singular Values)
큰 특이값들은 중요한 정보(패턴)를 나타냄 . 작은 특이값들은 노이즈(이상치 포함)를 나타낼 가능성이 높음 .
Low-Rank 분해 X W = X ^ W ^ = X ^ L 1 L 2 + X ^ R ≈ X ^ L 1 L 2 ⏟ 16-bit low-rank branch + Q ( X ^ ) Q ( R ) ⏟ 4-bit residual . \mathbf{XW} = \hat{\mathbf{X}} \hat{\mathbf{W}} = \hat{\mathbf{X}} \mathbf{L}_1 \mathbf{L}_2 + \hat{\mathbf{X}} \mathbf{R}\approx \underbrace{\hat{\mathbf{X}} \mathbf{L}_1 \mathbf{L}_2}_{\text{16-bit low-rank branch}}+ \underbrace{Q(\hat{\mathbf{X}}) Q(\mathbf{R})}_{\text{4-bit residual}}. XW = X ^ W ^ = X ^ L 1 L 2 + X ^ R ≈ 16-bit low-rank branch X ^ L 1 L 2 + 4-bit residual Q ( X ^ ) Q ( R ) .
대각 원소 중에서 상위 r개의 특이값만 유지 하여, 가장 중요한 정보만 포함하는 L1,L2를 생성.
→ 따로 16-bit 연산
남은 부분(작은 특이값) → R으로 분리
→ 4-bit 연산
→ 작은 특이값만 남았으므로 R을 4-bit로 양자화하더라도 정보 손실이 크게 줄어듦
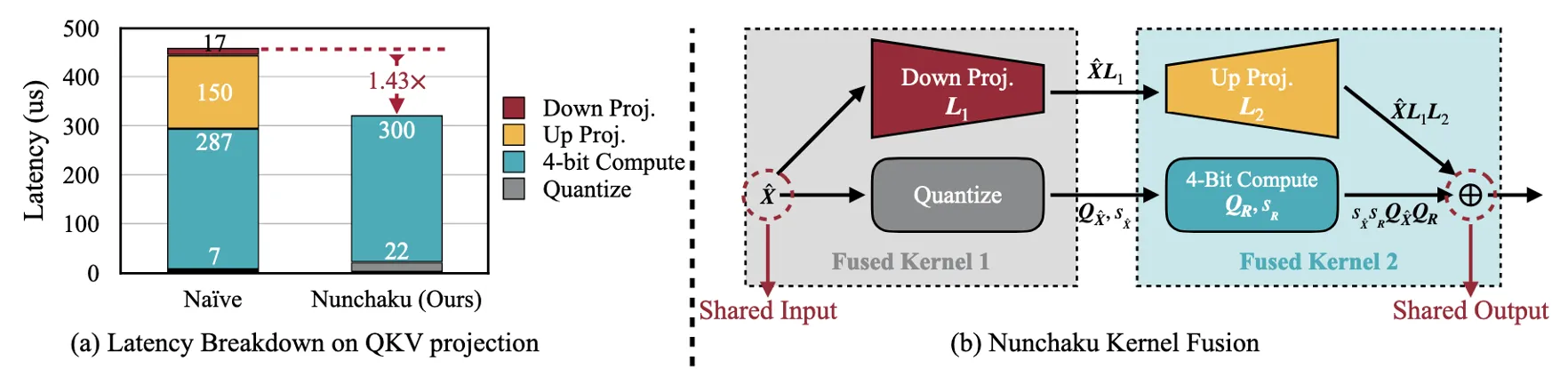
4.3 NUNCHAKU: Fusing Low-Rank and Low-Bit Branch Kernels Low-Rank Branch에서 발생하는 성능 저하 문제 QKV Projection과 같은 연산에서는 Low-Rank Branch가 L2 캐시를 초과하면서 DRAM에서 데이터를 불러와야 함 . 이는 메모리 접근 비용이 증가하여 연산 속도가 떨어지는 원인 . Figure 6(a)에서 보듯이, Low-Rank Branch는 전체 4-bit 연산 지연의 50%를 차지 . NUNCHAKU: 해결 방법 논문에서는 Low-Rank Branch와 Low-Bit Branch의 연산을 하나로 합쳐(fusing) 메모리 접근을 줄이는 방법을 제안 . Figure 6(b)에서 보듯이, 두 개의 Kernel을 합쳐서 데이터를 공유함 : Down Projection 연산을 Quantization Kernel과 합침 . Up Projection 연산을 4-bit 연산 Kernel과 합침 . 이를 통해 Low-Rank Branch가 Low-Bit Branch와 활성화값을 공유할 수 있어, 추가적인 메모리 접근을 제거 . 결과적으로, Kernel 호출 횟수가 절반으로 줄어들어 속도 개선 효과가 있음 .
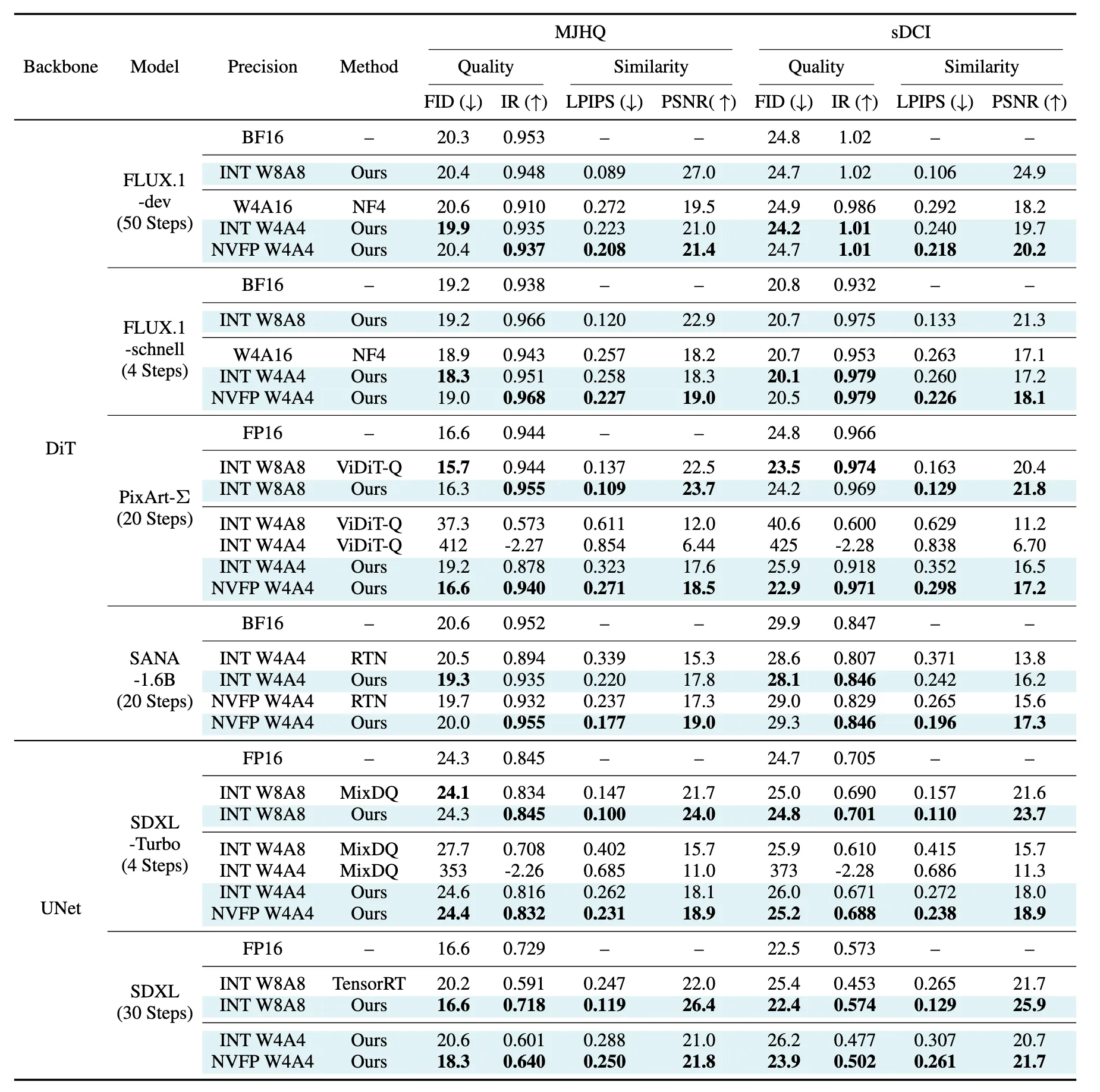
5 Experiments Benchmark models Model Architecture Parameters Special Features FLUX.1-dev DiT 12B 50-step guidance-distilled FLUX.1-schnell DiT 12B 4-step timestep-distilled PixArt-Σ DiT 600M 20-step default SANA DiT 1.6B 32× compression autoencoder, Linear Attention SDXL UNet 2.6B 30-step
Baselines Quantization Method Description Usage in Benchmarking NF4 Optimized 4-bit weight-only quantization assuming normal distribution Used as a weight-only quantization baseline for FLUX.1 ViDiT-Q Per-token quantization + smoothing to reduce outliers Achieves lossless 8-bit quantization on PixArt-Σ MixDQ Detects outliers in text embeddings and protects them with 16-bit pre-computation Enables W4A8 quantization with minimal performance drop on SDXL-Turbo TensorRT Industry-standard PTQ toolkit for 8-bit quantization Uses smoothing + percentile calibration over specific timesteps
Limitation 엄청난 기술이고 기술면에서는 한계가 없다고 생각함.
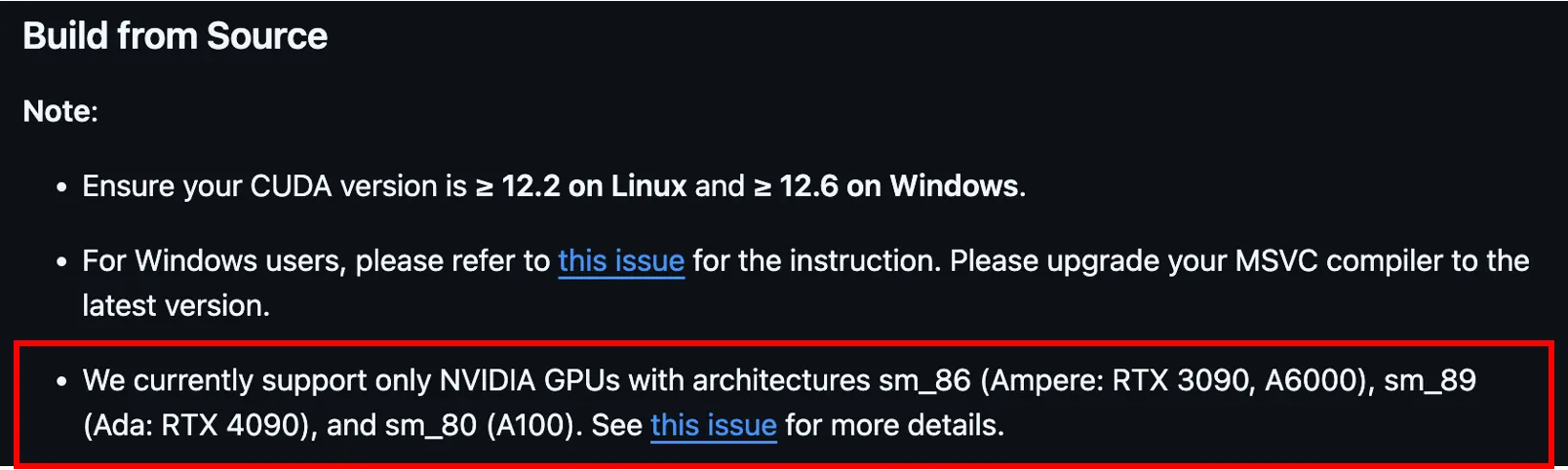
하지만, 굳이 한계점을 뽑자면, Song Han이 NVIDIA에서도 연구를 진행하기 때문에 NVIDIA chip만을 위해서 코드를 짰고, 이에 최적화되어있다.
심지어 CUDA 12.2 이상에서만 작동 가능해서 내 학교 서버로 돌려보려고 했는데, GPU Driver version이 낮아서 안돌아가더라.
물론 NVIDIA chip에서 극한의 최적화를 위해서 였지만, 다른 GPU 장비에서는 이를 사용할 수 없다.
같은 방식을 다른 GPU 장비와 Mobile edge device들에 적용한다면 좋을 것이다.
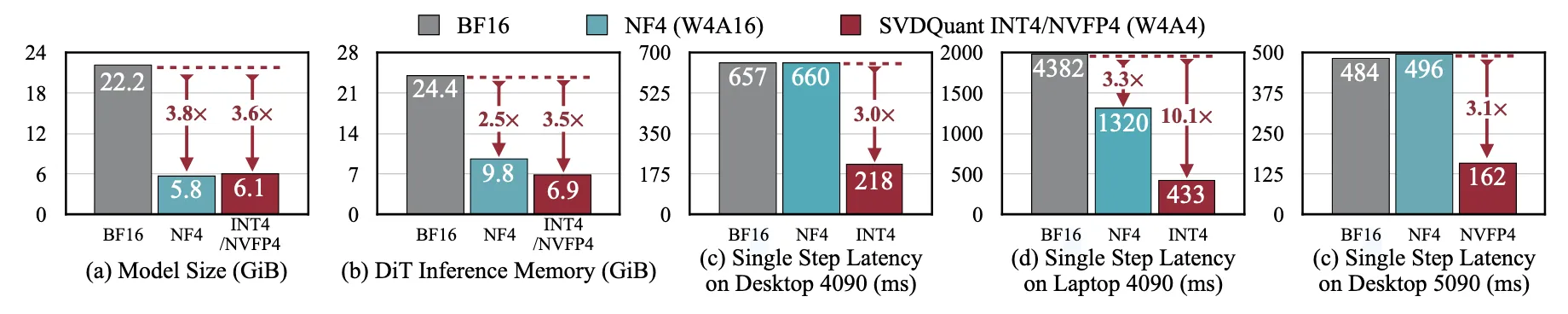
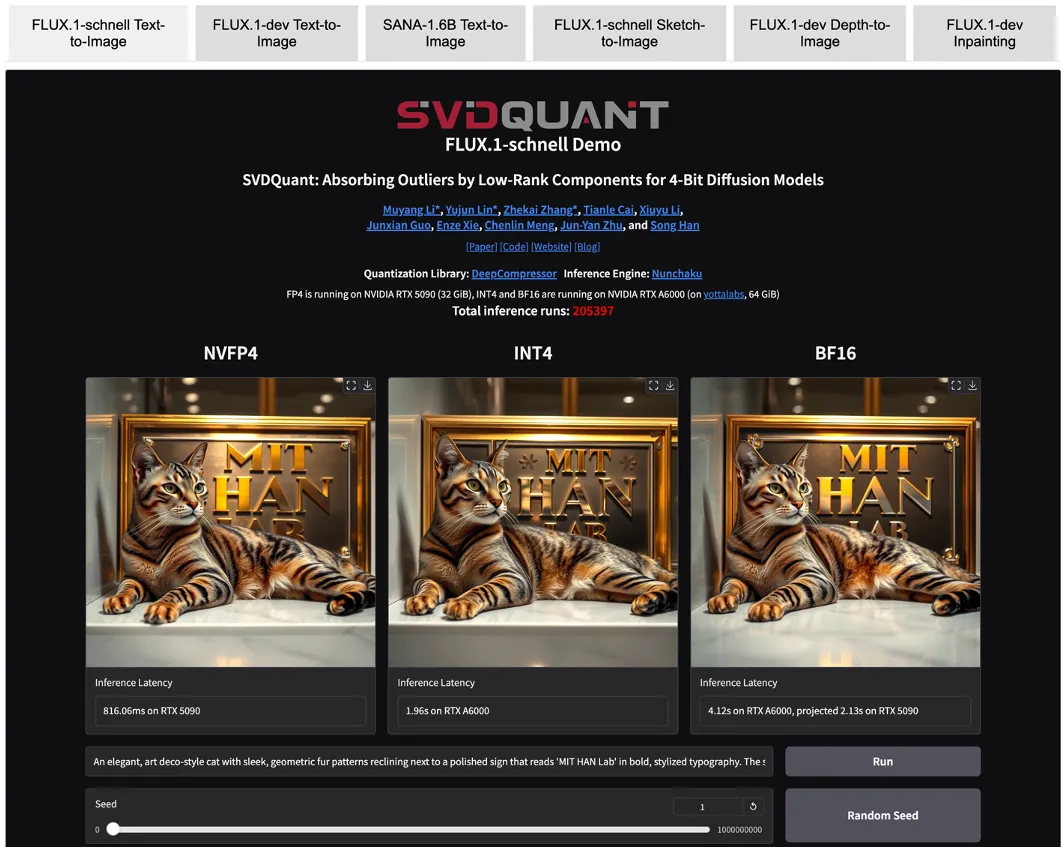
메모리랑 추론시간만 줄인게 아닌가? 정확도를 왜 언급? Memory, Latency? 아래 그림과 같이 SVD양자화로 인해 메모리와 latency 이점을 얻은게 포인트 아닌가?
비교가 기존 16bit / W4A16 / W4A4(SVD) 였기 때문에 큰 차이를 보여준 것 같다.
Inference time과 Memory 줄인게 포인트인줄 알았는데 완전 잘못 생각한것 같기도 합니다.
물론 Outlier때문에 32bit로 처리했던 부분들이 없어지고 16bit로 low rank로 따로 빼니까 향상은 됐을 것이지만, 제 생각에는 SVD 없는 W4A4랑 비교했다면, Memory와 추론시간이 3배 이상 차이나지는 않을 것입니다.
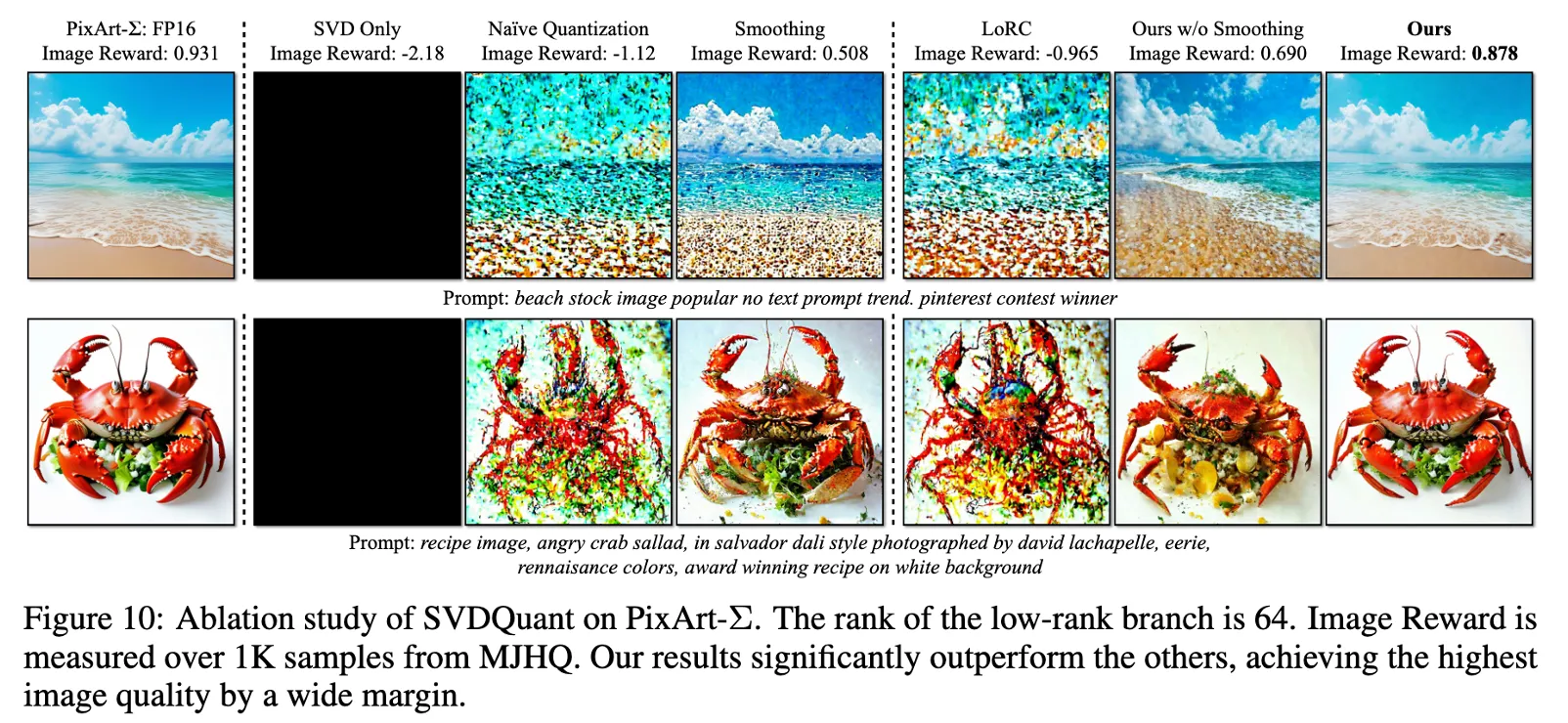
정확도? 기존 양자화에서 정확도를 유지하는 부분이 아래 그림처럼 많이 떨어졌었다.
(두번째가 기존 양자화 기법, 심지어 W4A4가 아닌 W4A16인데도 더 떨어지는 모습을 보임)
보존 할 수 있었던 이유 → Low-Rank Branch 기존 4-bit 양자화 방식에서는 Weight 전체를 4-bit로 변환 하므로 정보 손실이 큼. SVDQuant는 Weight를 Low-Rank Component (L1L2) 와 잔여 (R)로 분해한다. X W = X ^ W ^ = X ^ L 1 L 2 + X ^ R ≈ X ^ L 1 L 2 ⏟ 16-bit low-rank branch + Q ( X ^ ) Q ( R ) ⏟ 4-bit residual . \mathbf{XW} = \hat{\mathbf{X}} \hat{\mathbf{W}} = \hat{\mathbf{X}} \mathbf{L}_1 \mathbf{L}_2 + \hat{\mathbf{X}} \mathbf{R}\approx \underbrace{\hat{\mathbf{X}} \mathbf{L}_1 \mathbf{L}_2}_{\text{16-bit low-rank branch}}+ \underbrace{Q(\hat{\mathbf{X}}) Q(\mathbf{R})}_{\text{4-bit residual}}. XW = X ^ W ^ = X ^ L 1 L 2 + X ^ R ≈ 16-bit low-rank branch X ^ L 1 L 2 + 4-bit residual Q ( X ^ ) Q ( R ) . L1L2는 16-bit precision으로 유지 → 중요한 정보는 고정밀도로 남겨둠. 잔여 R만 4-bit로 양자화하여 정보 손실을 최소화함 한 번만 Low-Rank 분해하는 것이 아니라, 반복적으로 R을 최적화 하여 양자화 오류를 최소화
quantization error ∥ X ^ W ^ − ( X ^ L 1 L 2 + Q ( X ^ ) Q ( R ) ) ∥ F = ∥ X ^ R − Q ( X ^ ) Q ( R ) ∥ F = E ( X ^ , R ) , \left\| \hat{\mathbf{X}} \hat{\mathbf{W}} - \left( \hat{\mathbf{X}} \mathbf{L}_1 \mathbf{L}_2 + Q(\hat{\mathbf{X}}) Q(\mathbf{R}) \right) \right\|_F= \left\| \hat{\mathbf{X}} \mathbf{R} - Q(\hat{\mathbf{X}}) Q(\mathbf{R}) \right\|_F= E(\hat{\mathbf{X}}, \mathbf{R}), X ^ W ^ − ( X ^ L 1 L 2 + Q ( X ^ ) Q ( R ) ) F = X ^ R − Q ( X ^ ) Q ( R ) F = E ( X ^ , R ) , 이 식에서 L1L2+R로 분해함으로서 Quantization을 진행하면서 발생하는 Error를 최대한 줄인거임.
Quantization 자체가 Outlier로 인해서 정확도를 떨어뜨릴 수 밖에 없는데, 이를 최대한 보존했다는 점이 엄청난 연구인 것임!!!!
SVD를 LLM에 써도 되는가? 왜 Diffusion으로 논문을? 기존 제 생각 : 적용 할 수는 있을 것 같으나, LLM은 병목현상이 무거운 모델을 불러오는 과정 에서 나타나므로 뒤에 연산을 줄여도 Diffusion만큼 큰 효과는 나타날 지 모르겠습니다. (Diffusion은 연산이 병목 임)
물론 기존 제 생각도 찾아보니 맞는 것 같으나, 실제로 활용한다면, 바로 위 질문에서 다뤘던 정확도 향상에도 도움이 되기 때문에, 오히려 정확도 부분에서 도움이 될 것 같습니다.
기존 양자화 GPTQ → Post-training quantization 방식, Weight만 4-bit 변환. AWQ → Weight 중요도를 분석해 선택적으로 4-bit 변환. SmoothQuant → Activation 이상치를 Weight로 이동시켜 양자화 오류를 줄이는 방식.
SVDQuant 사용한다면? Weight를 Low-Rank(16-bit) + Residual(4-bit)로 나누어 중요한 정보는 유지하면서 압축하므로
Diffusion처럼 정확도 향상에 도움이 될듯 !!!
For an explanation from the author, Song Han Youtube [Introduction to SVDQuant for 4-bit Diffusion Models]
Demo https://hanlab.mit.edu/projects/svdquant